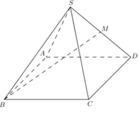
Cho hình chóp tứ giác đều S . A B C D có tất cả các cạnh bằng a. Gọi M là trung điểm SD (tham khảo hình vẽ bên) Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
A. 2 2
B. 3 3
C. 2 3
D. 1 3
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A, B, C, D là
A. 4
B. 2
C. 3
D. 1
Đáp án C
Có 3 mặt phẳng. 2 mặt phẳng là các mặt đi qua điểm S và qua các đường trung trực của AB và AD.1 mặt phẳng qua S và song song với mặt phẳng (ABCD)
Cho hình chóp tứ giác đều S . A B C D . Số mặt phẳng qua điểm S cách đều các điểm A, B, C, D là
A. 4
B. 2
C. 3
D. 1
Đáp án C
Có 3 mặt phẳng. 2 mặt phẳng là các mặt đi qua điểm S và qua các đường trung trực của AB và AD.1 mặt phẳng qua S và song song với mặt phẳng A B C D .
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
A. 4
B. 2
C. 3
D. 1
Cho hình chóp tứ giác đều S.ABCD . Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
A. 4
B. 2
C. 3
D. 1
Khẳng định nào sau đây là sai?
Các hình chóp sau đây luôn có các đỉnh nằm trên một mặt cầu:
A. Hình chóp tam giác B. Hình chóp ngũ giác đều
C. Hình chóp tứ giác D. Hình chóp đều n-giác.
Chọn C.
Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Chọn C vì điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Khối chóp tứ giác S.ABCD có đáy là hình bình hành. Có bao nhiêu mặt phẳng cách đều cả 5 điểm S, A, B, C, D?
A. 5
B. 11
C. 9
D. 3
Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D:
Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
Mặt phẳng đi qua tâm O và song song với từng mặt bên : có 4 mặt như vậy
Cho hình chóp tứ giác đều S. ABCD có cạnh AB=10cm. Cạnh bên SA=12cm a) tính đường chéo AC b) tính đường cao SO c) tính thể tích hình chóp
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Tính diện tích toàn phần của các hình chóp đều sau đây :
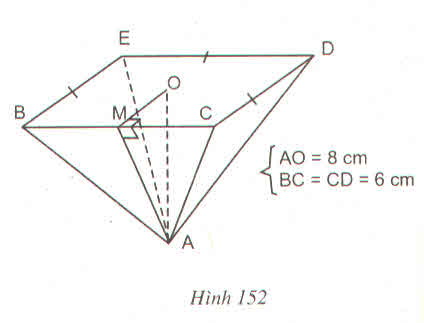
a) Hình cho theo các kích thước trên hình 152
b) Hình chóp tứ giác đều, cạnh đáy 6cm, chiều cao hình chóp 5cm
c) Hình chóp tứ giác đều, cạnh đáy 20cm, chiều cao hình chóp 7cm
d) Hình chóp tứ giác đều, cạnh đáy 1m, chiều cao hình chóp 50cm
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và khoảng cách từ A đến (SBC) bằng a 6 3 . Thể tích của hình chóp bằng:
A. 6 24 a 3 B. 2 9 a 3
C. 2 8 a 3 D. 2 6 a 3
Chọn D.
Gọi H, M, N theo thứ tự là các trung điểm của các cạnh AC, BC, AD.
Kẻ NI ⊥ SM (I ∈ SM). Để ý rằng AN // (SBC)
Do đó NI = d(N,(SBC)) = d(A,(SBC)) = a 6 3
Từ hai tam giác đồng dạng SHM và NIM ta tính được SH.