Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D:
Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.
Mặt phẳng đi qua tâm O và song song với từng mặt bên : có 4 mặt như vậy
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Dựng mặt phẳng (P) cách đều năm điểm A, B, C, D và S. Hỏi có tất cả bao nhiêu mặt phẳng (P) như vậy?
A. 2 mặt phẳng
B. 5 mặt phẳng
C. 1 mặt phẳng
D. 4 mặt phẳng
Cho hình chóp tứ giác S . A B C D đáy là hình bình hành có thể tích bằng V . Lấy điểm B , , D , lần lượt là trung điểm của các cạnh S B và S D . Mặt phẳng A B , D , cắt cạnh S C tại C , . Khi đó thể tích khối chóp S . A B , C , D , bằng
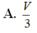
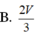
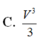
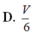
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng (SCD) bằng 3 7 a 7 . Tính thể tích V của khối chóp S.ABCD.
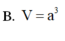
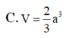
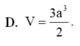
Cho hình chóp tứ giác S. ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S. AB'C'D' bằng:
A. V 3
B. 2 V 3
C. V 3 3
D. V 6
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
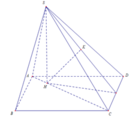
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD có tất cả các cạnh bằng a và có tâm O. Gọi M là trung điểm của OA. Tính khoảng cách d từ M đến mặt phẳng (SCD) được :
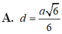
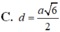
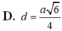
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện ( H 1 ) và ( H 2 ) trong đó ( H 1 ) chứa điểm C. Thể tích của khối ( H 1 ) là
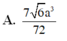
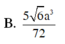
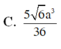
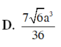
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC=a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2a 6 . Tính thể tích V của khối chóp S.ABCD?
