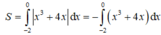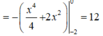Cho hình D giới hạn bởi các đường y = x 2 − 2 và y = − x . Khi đó diện tích của hình D là:
A. 13 3 .
B. 7 3 .
C. 7 π 3 .
D. 13 π 3 .
Cho hình D giới hạn bởi các đường y = x 2 − 2 và y = − x . Khi đó diện tích của hình D là
A. 13 3 .
B. 7 3 .
C. 7 π 3 .
D. 13 π 3 .
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
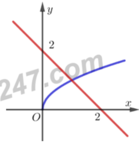
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Diện tích hình phẳng giới hạn bởi các đường thẳng y = - x , n ế u x ≤ 1 x - 2 , n ế u x > 1 và y = 10 3 x - x 2 là a/b . Khi đó a + 2b bằng
A. 16
B. 15
C. 17
D. 18
Chọn C.
Ta có 10 3 x - x 2 = - x ⇒ x = 0 10 3 x - x 2 = x - 2 ⇒ x = 3
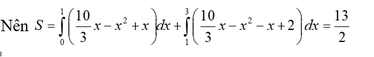
Suy ra a=13 ; b=2 và a+2b=17.
Cho (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình y = 10 3 x - x 2 , y = - x k h i x ≤ 1 x - 2 k h i x > 1 . Diện tích của (H) bằng
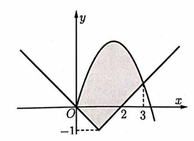
A. 5,5
B. 6,5
C. 11/6
D. 14/3
Cho hình phẳng (D) giới hạn bởi các đường y = ( x - 2 ) 2 và y = 4 . Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Oy
A. 219 π 2
B. 172 π 5
C. 113 π 2
D. 128 π 3
Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t
Hình phẳng giới hạn bởi đồ thị hàm số y = e x . sin x và các đường thẳng x = 0, x = π, trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 , S 2 sao cho ( 2 S 1 + 2 S 2 - 1 ) = ( 2 S 1 - 1 ) 2 khi đó k bằng:
A. π 4
B. π 2
C. π 3
D. π 6
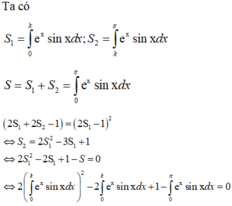
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án B
Diện tích hình phẳng giới hạn bởi các đường y = 1 + ln x x , y = 0 , x = 1 và x = e là S = a 2 + b . Khi đó giá trị a 2 + b 2 là:
A. 2 3 .
B. 4 3 .
C. 20 9 .
D.2
Đáp án C
Ta có S = ∫ 1 e 1 + ln x x d x . Đặt 1 + ln x = t ⇒ ln x = t 2 − 1 ⇒ 1 x = d x = 2 t d t
Đổi cận: x = 1 ⇒ t = 1 ; x = e ⇒ t = 2
⇒ S = ∫ 1 2 t .2 t d t = 2 t 3 3 2 1 = 4 2 3 − 2 3 = 4 2 − 2 3 ⇒ a = 4 3 b = − 2 3
⇒ a 2 + b 2 = 16 9 + 4 9 = 20 9
Diện tích hình phẳng giới hạn bởi các đường y = 1 + ln x x , y=0, x=1 và x=e là S = a 2 + b . Khi đó giá trị a 2 + b 2 là:
A. 2 3
B. 4 3
C. 20 9
D. 2
Diện tích hình phẳng được giới hạn bởi các đường y = x 3 + 3 x , y = - x và đường thẳng x = -2 là:
A. -12(dvdt).
B. 12(dvdt).
C. 4(dvdt).\
D. -4(dvdt).
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó: