Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) và SB=a 3 . Tính thể tích khối chóp S.ABCD
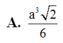
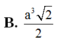
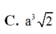
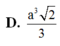
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. S A ⊥ A B C D và S B = a 3 . Thể tích khối chóp S.ABCD là
A. a 3 2 4
B. a 3 2 2
C. a 3 2 6
D. a 3 2 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm cạnh AD, cạnh SB hợp với đáy một góc 60 ° . Tính theo a thể tích V của khối chóp S.ABCD
A. a 3 15 6
B. a 3 5 4
C. a 3 15 6 3
D. a 3 15 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD; cạnh bên SB hợp với đáy một góc 60 o Tính theo a thể tích V của khối chóp S.ABCD.
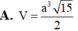
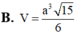
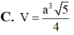
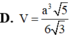
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S A ⊥ A B C D và S B = a 3 . Tính thể tích khối chóp
A. a 3 2 6
B. a 3 2 2
C. a 3 2
D. a 3 2 3
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD) và SB= a 3 . Thể tích khối chóp S.ABCD là:
A. a 3 2 2
B. a 3 2 6
C. a 3 2
D. a 3 2 3
Đáp án D
Ta có:
S A B C D = a 2
S A 2 = S B 2 - A B 2 = 3 a 2 - a 2 = 2 a 2 ⇒ S A = a 2
Do đó
V S . A B C D = 1 3 . S A . S A B C D = 1 3 a 2 . a 2 = a 3 2 3
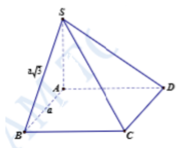
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc B A D ^ = 60 o và S A = S B = S D = a 3 2
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
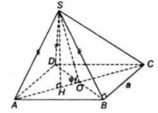
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
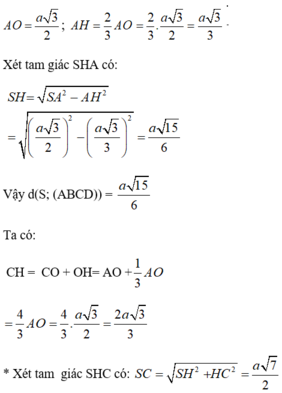

Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy SA= a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
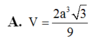
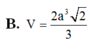
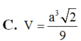
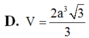
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy S A = a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3