Tính diện tích vải cần có để may một cái mũ có dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể riềm, mép)
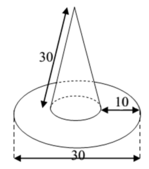
A. 350 π
B. 400 π
C. 450 π
D. 500 π
Tính diện tích vải cần có để may một cái mũ có dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể riềm, mép)
A. 350 π
B. 400 π
C. 450 π
D. 500 π
Đáp án A
S
=
π
.15
2
−
π
5
2
+
π
.5.30
=
350
π
Tính diện tích vải tối thiểu để may được một chiếc mũ có hình dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể viền, mép) biết phía trên có dạng một hình nón và phía dưới (vành mũ) có dạng hình vành khăn.
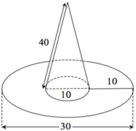
A. 450π.
B. 500π.
C. 350π.
D. 400π.
Tính diện tích vải tối thiểu để may được chiếc mũ có hình dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể viền, mép) biết phía trên có dạng hình nón và phía dưới (vành mũ) có dạng hình vành khăn.
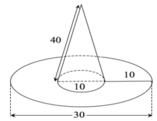
![]()
![]()
![]()
![]()
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
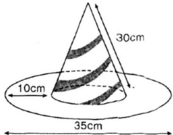
Hình 97
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: 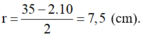
Diện tích xung quanh hình nón: Sxq = π.r.l = π.7,5.30 = 225π (cm2)
Diện tích vành nón (hình vành khăn): 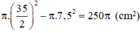
Diện tích vải cần để may: 225π + 250π = 475π ≈ 1492,3 (cm2)
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
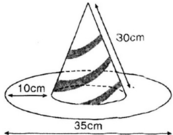
Hình 97
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: 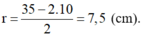
Diện tích xung quanh hình nón: Sxq = π.r.l = π.7,5.30 = 225π (cm2)
Diện tích vành nón (hình vành khăn): 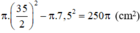
Diện tích vải cần để may: 225π + 250π = 475π ≈ 1492,3 (cm2)
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h. 97). Hãy tính tổng diện tích vải cần có để làm lên cái mũ (không kể riềm, mép, phần thừa).
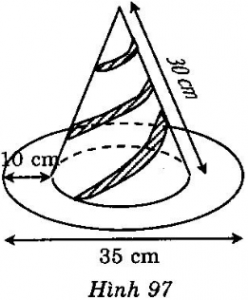
Giải:
Diện tích vải cần có để làm nên cái mũ diện tích xung quanh của hình nón và diện tích vành nón.
(cm)
Vậy diện tích vải cần có là:
S = Sxq + SVành nón = 706,5 + 785 = 1491,5 (cm2)
Một cái mũ bằng vải của nhà ảo thuật với các kích thước như hình vẽ dưới đây. Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không kể viền, mép, phần thừa).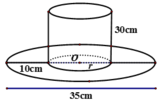
![]()
![]()
![]()
![]()
Một cái mũ bằng vải của nhà ảo thuật gia gồm phần dạng hình trụ (có tổng diện tích vải là S 1 ) và phần dạng hình vành khăn (có tổng diện tích vải là S 2 ) với các kích thước như hình vẽ. Tính tổng r + d sao cho biểu thức P = 3 S 2 − S 1 đạt giá trị lớn nhất. (Không kể viền, mép, phần thừa).
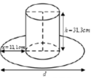
A. 28,6
B. 26,2
C. 30,8
D. 28,2
Đáp án D
Diện tích S 1 là S 1 = 2 π r h + π r 2 = 62 , 6 π r + π r 2 ( diện tích toàn phần trừ một đáy)
Diện tích S 2 là S 2 = π 11 , 1 + r 2 − π r 2 = π 123 , 21 + 22 , 2 r ( diện tích hình tròn to trừ hình tròn nhỏ)
Khi đó:
P = 3 S 2 − S 1 = 3 π 22 , 2 r + 123 , 21 − 62 , 6 π r − π r 2 = 369 , 63 π + 4 π r − π r 2
Ta có:
4 r − r 2 = 4 − 2 − r 2 ≤ 4 ⇔ π 4 r − r 2 ≤ 4 π ⇒ P ≤ 373 , 63 π
Dấu “=” xảy ra khi và chỉ khi:
r = 2 ⇒ d = 2 x + r = 2 11 , 1 + 2 = 26 , 2 ⇒ r + d = 28 , 2
Một cái nhà kính trồng cây thí nghiệm có dạng một lăng trụ đứng có các kích thước như ở hình 148. EDC là một tam giác cân.
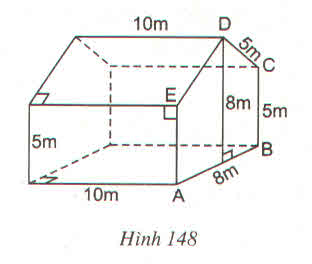
Hãy tính :
a) Diện tích hình ABCDE
b) Thể tích nhà kính
c) Diện tích kính cần phải có để "lợp" hai mái và bốn bức tường nhà (không tính riềm, mép,.....)
a: \(S_{ABCDE}=\dfrac{2\left(5+8\right)}{2}\cdot4=52\left(m^2\right)\)
b: \(V=S\cdot h=52\cdot10=520\left(m^{^3}\right)\)
c: Diện tích bốn hình chữ nhật là \(5\cdot10\cdot4=200\left(m^2\right)\)
Tổng diện tích cần dùng là:
200+52x2=304(m2)