Cho số phức z, w khác 0 sao cho z − w = 2 z = w . Phần thực của số phức u = z w là
A. a = − 1 8
B. a = 1 4
C. a = 1
D. a = 1 8
Cho số phức z, w khác 0 sao cho |z-w| = 2|z| = |w|. Phần thực của số phức u = z w là
A. a = - 1 8
B. a = 1 4
C. a = 1
D. a = 1 8
Đáp án D
Giả sử ![]()
Từ giả thiết đầu bài |z-w| = 2|z| = |w|, ta có hệ sau
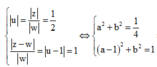
![]()
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho hai số phức z và w khác 0 thoả mãn|z+3w|=5|w| và |z-2wi|=|z-2w-2wi| Phần thực của số phức z/w bằng
A.1.
B.-3.
C.-1.
D.3
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho các số phức z, w khác 0 thỏa mãn z+w khác 0 và 1 z + 3 w = 6 z + w Khi đó z w bằng
![]()
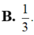
![]()
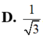
Cho hai số phức z và w z ≠ 0, w ≠ 0 . Biết z − w = z + w . Khi đó điểm biểu diễn số phức z w
A. thuộc trục Ox
B. thuộc đường phân giác của góc phần tư thứ nhất và thứ ba.
C. thuộc trục Oy
D. thuộc đường phân giác của góc phần tư thứ hai và thứ tư
Đáp án C
Đặt z = x + y i ; w = a + b i , x ; y ; a ; b ∈ ℝ
z − w = z + w ⇔ x + y i − a − b i = x + y i + a + b i
⇔ x − a 2 + y − b 2 = x + a 2 + y + b 2 ⇔ a x + b y = 0
Mặt khác
z w = x + y i a + b i = x + y i a − b i a 2 + b 2 = − a y + b x i a 2 + b 2
Suy ra z w là một số thuần ảo, vậy điểm biểu diễn số phức z w thuộc trục Oy
Cho hai số phức z và w z ≠ 0 , w ≠ 0 . Biết z − w = z + w . Khi đó điểm biểu diễn số phức z w
A. thuộc trục Ox.
B. thuộc đường phân giác của góc phần tư thứ nhất và thứ ba.
C. thuộc trục Oy.
D. thuộc đường phân giác của góc phần tư thứ hai và thứ tư.