Cho hàm số y = f x có đạo hàm trên và có đồ thị là đường cong trong hình vẽ bên.
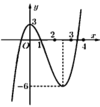
Đặt g x = f f x . Tìm số nghiệm của phương trình g ' x = 0
A. 2
B. 8
C. 4
D. 6
Cho hàm số y=f(x) có đạo hàm trên ℝ và có đồ thị là đường cong trong hình vẽ dưới. Đặt g(x) = f[f(x)]. Tìm số nghiệm của phương trình g'(x)=0
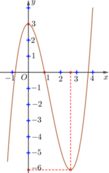
A. 2
B. 8
C. 4
D. 6
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt g(x)=f [f(x)]. Tìm số nghiệm của phương trình g'(x) = 0
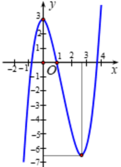
A. 4
B. 6
C. 2
D. 8
Ta có
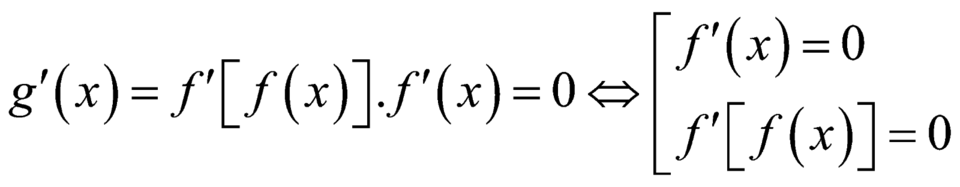
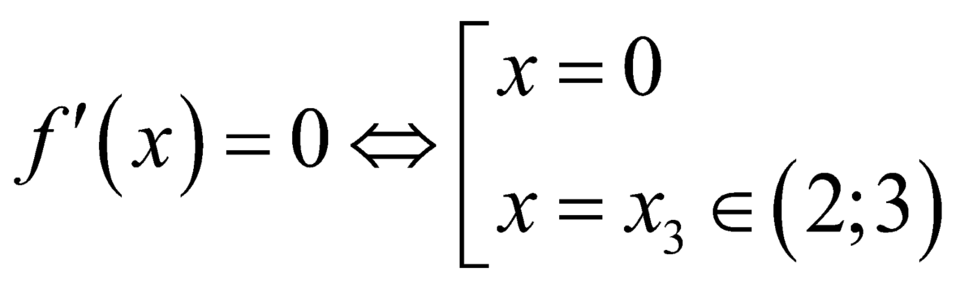
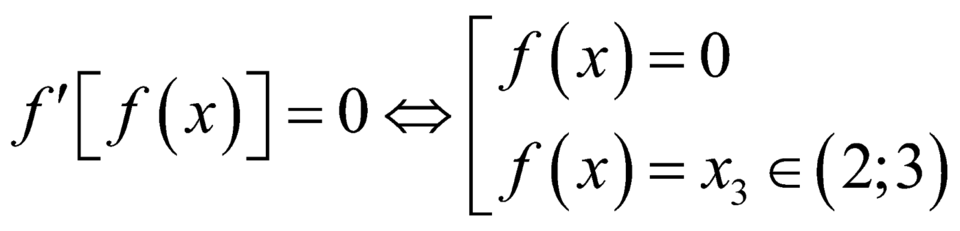
+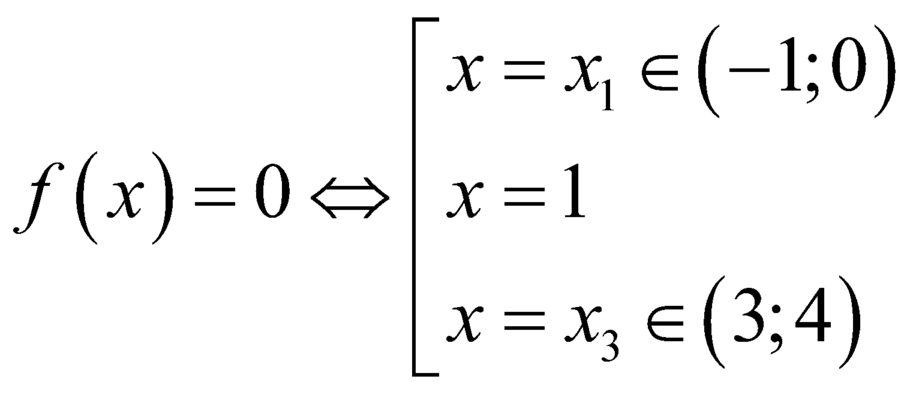
+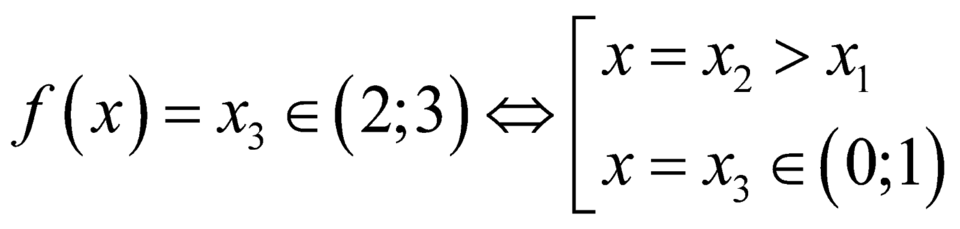 .
.
Vậy phương trình ![]() có 8 nghiệm phân biệt.
có 8 nghiệm phân biệt.
Đáp án D
Cho hàm số y= f(x) có đạo hàm trên R. Đường cong trong hình vẽ dưới là đồ thị của hàm số y= f’(x) . Xét hàm số g( x) = f( 3-x2).
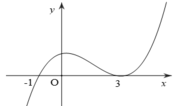
Mệnh đề nào dưới đây là đúng?
A. Hàm số y= g( x) đồng biến trên
B. Hàm số y= g( x) đồng biến trên (0 ;3)
C. Hàm số y= g(x) nghịch biến trên
D. Hàm số y= g(x) nghịch biến trên ![]() và (0;2)
và (0;2)
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt g x = f x 2 Tìm số nghiệm của phương trình g'(x)=0

A. 5
B. 4
C. 3
D. 2
Cho hàm số y = f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x), (y = f’(x) liên tục trên R). Xét hàm số g(x) = f(x2 - 2). Mệnh đề nào dưới đây sai?

A. Hàm số g(x) nghịch biến trên (-∞;-3)
B. Hàm số g(x) có 3 điểm cực trị
C. Hàm số g(x) nghịch biến trên (-1;0)
D. Điểm cực đại của hàm số là 0
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x). Xét hàm số g(x) = f(x2 – 3). Mệnh đề nào dưới đây sai ?
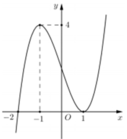
A. Hàm số g(x) đồng biến trên (–1;0)
B. Hàm số g(x) nghịch biến trên (–∞;–1)
C. Hàm số g(x) nghịch biến trên (1;2)
D. Hàm số g(x) đồng biến trên (2;+ ∞)
Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
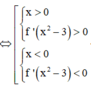
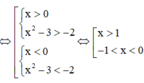
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)
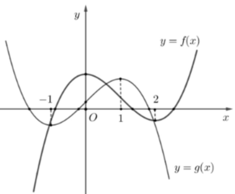
Cho hai hàm số y=f(x); y=g(x) có đạo hàm trên R và có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Biết rằng hai hàm số y=f(-2x+1) và y = g a x + b a b ∈ ℝ ; a # 0 có cùng khoảng đồng biến. Giá trị của a + 2b bằng
A. 3
B. 4
C. 2
D. 6
Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 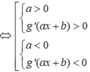
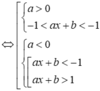
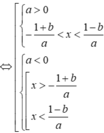
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
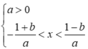 và
và 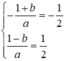
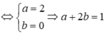
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong hình bên. Hàm số g(x) = f (3x - 2) nghịch biến trên khoảng
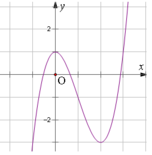
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) liên tục và có đạo hàm cấp hai trên R. Đồ thị của các hàm số y = f(x), y = f'(x) và y = f''(x) lần lượt là các đường cong nào trong hình vẽ bên.
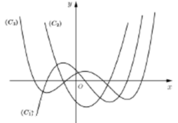
A. C 1 , C 3 , C 2
B. C 3 , C 2 , C 1
C. C 3 , C 1 , C 2
D. C 1 , C 2 , C 3
Đáp án C
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị C 3 có dạng đồ thị hàm số trùng phương.
Đồ thị C 2 có dạng đồ thị hàm số bậc hai (parabol)
Đồ thị C 1 có dạng đồ thị hàm số bậc ba
Vậy đồ thị của các hàm số
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong hình vẽ bên là đồ thị hàm số y=f '(x) (Hàm số y=f '(x) liên tục trên R. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây là sai?
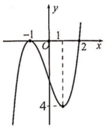
A. Hàm số y=g(x) đồng biến trên khoảng (-2;-1)
B. Hàm số y=g(x) đồng biến trên khoảng 2 ; + ∞
C. Hàm số y=g(x) nghịch biến trên khoảng (-1;0)
D. Hàm số y=g(x) nghịch biến trên khoảng (0;2)