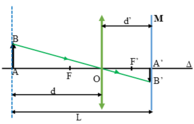
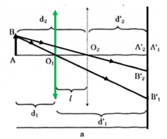
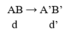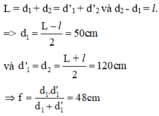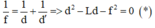Đặt một vật sáng song song và cách màn M một đoạn 2m (hình ). Một thấu kính được đặt luôn song song với màn M, di chuyển thấu kính trong khoảng giữa vật và màn thì thu được hai vị trí cho ảnh rõ nét và cách nhau 40cm. Tiêu cự của thấu kính này là
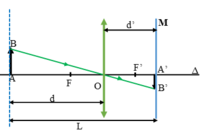
A. 25cm
B. 48cm
C. 80cm
D. 50cm