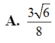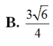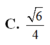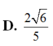Tính thể tích V của khối chóp S.ABC có độ dài các cạnh, SA=BC=5a, SB=AC=6a và SC=AB=7a
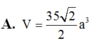
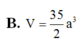
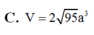
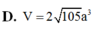
Cho hình chóp S.ABC có A B = 6 a ; A C = 4 a ; S A = S B = S C = B C = 5 a . Tính thể tích
V khối chóp S.ABC theo
A. V = 5 a 3 111 4
B. V = 15 a 3 111 4
C. V = 5 a 3 111 12
D. V = 45 a 3 111 4
Đáp án A
Gọi H là hình chiếu của S lên (ABC) suy ra H là tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng công thức Hê – rông, tính được S A B C = 15 a 2 7 4

Cho hình chóp S.ABC có AB = 6a, AC = 4a; SA = SB = SC = BC = 5a. Tính thể tích V khối chóp S.ABC theo a
A. 5 a 3 111 4
B. 15 a 3 111 4
C. 5 a 3 111 12
D. 45 a 3 111 4
Đáp án A
Gọi H là hình chiếu của S lên (SAB) suy ra H là tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng công thức Hê – rông, tính được
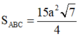
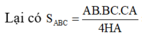
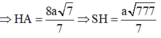
Thể tích khối chóp:
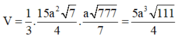
Phương án nhiễu.
B. Chưa nhân 1/3.
Cho hình chóp S.ABC có độ dài các cạnh: S A = B C = x , S B = A C = y , S C = A B = z thỏa mãn x 2 + y 2 + z 2 = 12 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
A. 2 3
B. 8 3
C. 2 2 3
Đáp án C
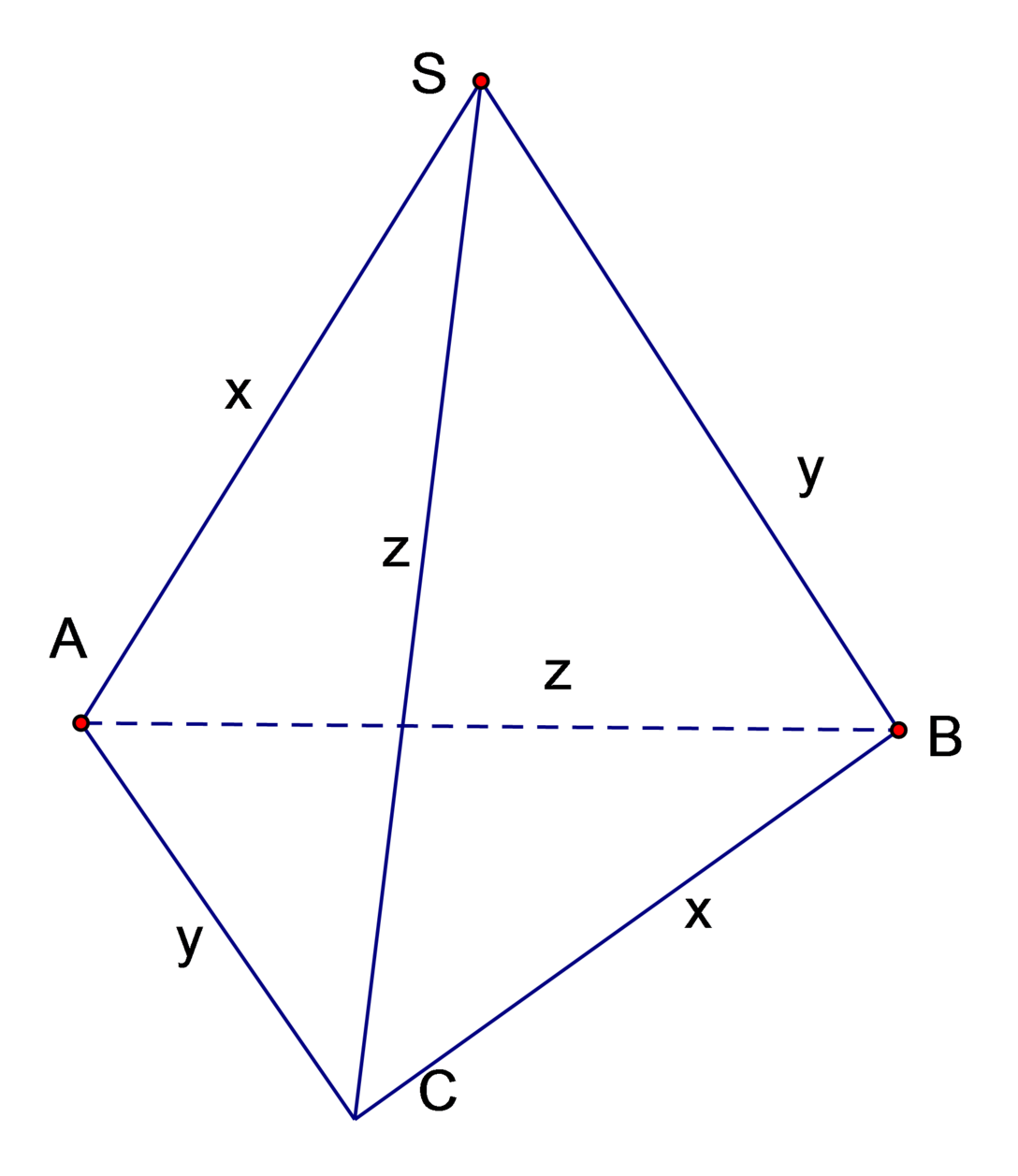
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:
V S A B C = 1 6 2 x 2 + y 2 − z 2 y 2 + z 2 − x 2 z 2 + x 2 − y 2 ≤ 1 6 2 x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + z 2 + x 2 − y 2 3 3 = 1 6 2 x 2 + y 2 + z 2 3 3 = 1 6 2 12 3 3 = 1 6 2 .8 = 2 2 3
Như vậy V S A B C lớn nhất bằng 2 2 3 khi: x=y=z=2
Cho hình chóp S.ABCD có AB=3a, AC=4a, BC=5a, SA=SB=SC=6a.Tính thể tích V của khối chóp S.ABC?
A. V = 119 a 3
B. V = 119 3 a 3
C. V = 4 119 3 a 3
D. V = 4 119 a 3
Đáp án A
Hướng dẫn giải:
Vì AB = 3a,AC = 4a, BC = 5a nên tam giác ABC vuông tại A.
Gọi H là hình chiếu của S lên mặt phẳng (ABC)
Vì SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC và chính là trung điểm của BC.
Do đó S H = S B 2 - H B 2 = 119 a 2 .
Diện tích tam giác ABC là S ∆ A B C = 6 a 2 .
Kết luận thể tích khối chóp
V S . A B C = 1 3 . 6 a 2 . 113 2 a = a 3 119
Cho hình chóp S.ABC có độ dài các cạnh SA=BC=x, SB=AC=y, SC=AB=z thỏa mãn x 2 + y 2 + z 2 = 12 . Giá trị lớn nhất của thể tích khối chóp S.ABC là:
A. V = 2 2 3
B. V = 2 3 3
C. V = 2 3
D. V = 3 2 2
Đáp án A
Thể tích khối chóp S.ABC là:
V S . A B C = 2 12 . x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
Mà: x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
≤ x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + x 2 + z 2 − y 2 27
= x 2 + y 2 + z 2 3 27
Suy ra: S . A B C ≤ 2 12 . x 2 + y 2 + z 2 27
= 2 12 . 12 3 27 = 2 2 3
Vậy: V max = 2 2 3
Cho hình chóp S.ABC có các cạnh S A = B C = 3 ; S B = A C = 4 ; S C = A B = 2 5 . Tính thể tích khối chóp S.ABC.
A. 390 12
B. 390 6
C. 390 8
D. 390 4
Đặt
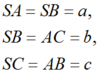
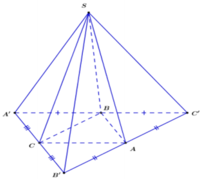
Dựng hình chóp S . A ' B ' C ' sao cho A, B, C lần lượt là trung điểm của B ' C ' ; C ' A ' ; A ' B ' .
Dễ thấy đồng dạng với ∆ A ' B ' C ' theo tỉ số
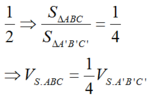
Ta có AB, BC, CA là các đường trung bình của tam giác A ' B ' C '
![]()
là các tam giác vuông tại S (Tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy)
⇒ S A ' ; S B ' ; S C ' đôi một vuông góc
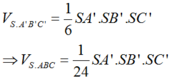
Áp dụng định lí Pytago ta có:
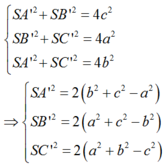
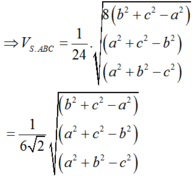
Thay
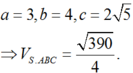
Chọn D.
Cho hình chóp S.ABC có độ dài cạnh SA = BC = x, SB = AC = y, SC = AB = z thỏa mãn điều kiện x 2 + y 2 + z 2 = 9 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
A. 3 6 8
B. 3 6 4
C. 6 4
D. 2 6 5
Đáp án C.
Ghép hình chóp vào hình hộp chữ nhật có 3 kích thước là a, b, c.
Ta có a 2 + b 2 = x 2 b 2 + c 2 = y 2 ⇒ a 2 + b 2 + c 2 = x 2 + y 2 + z 2 2 c 2 + a 2 = z 2 ⇒ c 2 = y 2 + z 2 - x 2 2 a 2 = x 2 + z 2 - y 2 2 b 2 = x 2 + y 2 - z 2 2
⇒ a b c = y 2 + z 2 - x 2 x 2 + z 2 - y 2 x 2 + y 2 - z 2 8 .
Thể tích khối chóp S.ABCD là V = 1 3 a b c = 12 12 y 2 + z 2 - x 2 x 2 + z 2 - y 2 x 2 + y 2 - z 2 .
≤ 1 6 2 y 2 + z 2 - x 2 + x 2 + z 2 - y 2 + x 2 + y 2 - z 2 3 3 = 1 6 2 . 3 3 = 6 4 .
Vậy giá trị lớn nhất của V S . A B C D là 6 4 .
Cho hình chóp S.ABC có độ dài cạnh SA=BC=x, SB=AC=y, SC=AB=z thỏa mãn điều kiện x 2 + y 2 + z 2 = 9 Tính giá trị lớn nhất của thể tích khối chóp S.ABC.

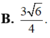
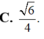
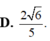
Cho hình chóp S.ABC có độ dài cạnh SA=BC=x, SB=AC=y, SC=AB=z thỏa mãn điều kiện x 2 + y 2 + z 2 = 9 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC