Tìm tất cả các giá trị của m để hàm số ![]() đồng biến trên
ℝ
đồng biến trên
ℝ
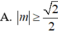

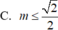

Tìm tất cả các giá trị thực của tham số m để hàm số ![]() đồng biến trên
ℝ
đồng biến trên
ℝ
A. Không có m
B. - 1 ≤ m ≤ - 1 2
C. m < - 1 2
D. m > - 1
Tìm tất cả các giá trị của m để hàm số y=cos2x+mx đồng biến trên ℝ .
A. 4
B. 2
C. 3
D. 1
Tìm tất cả các giá trị của để hàm số y = x + m ( sin x + cos x ) đồng biến trên ℝ
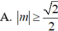
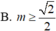
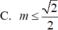
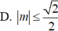
Tìm tất cả các giá trị của tham số m để hàm số y = x 3 + m + 1 x 2 + 3 x + 1 đồng biến trên ℝ
A. − 7 ≤ m ≤ 5
B. − 4 ≤ m ≤ 2
C. m ≤ − 4 hoặc m ≥ 2
D. m ≥ 2
Đáp án C
Ta có: y ' = − 1 − m x − 1 2 luôn âm hoặc luôn dương trên đoạn 2 ; 4 .
Để min 2 ; 4 y = 4 ⇒ y 2 = 4 y 4 = 4 ⇔ m + 2 = 4 m + 4 3 = 4 ⇔ m = 2 m = 8 .
Với m = 2 suy ra y ' < 0 nên min y 2 ; 4 = y 4 = 2 (loại)
Với m = 8 suy ra y ' < 0 nên min y 2 ; 4 = y 4 = 4
Tìm tất cả các giá trị thực của tham số m để hàm số y = 3 sin x - 2 cos x + m x đồng biến trên ℝ
A. m ∈ ( - ∞ ; 13 ]
B. m ∈ ( - 13 ; + ∞ ]
C. m ∈ ( 13 ; + ∞ ]
D. m ∈ ( - ∞ ; - 13 ]
Chọn C.
![]()
Ta có y ' = 3 cos x + 2 sin x + m
Để hàm số đồng biến trên ℝ thì y ' ≥ 0 , ∀ x ∈ ℝ
![]()
![]()
![]()
Với α là góc thỏa mãn
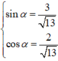
![]()
![]()
Vậy m ∈ ( 13 ; + ∞ ]
Tìm tất cả các giá trị thực của tham số m để hàm số y = 3 sin x - 2 cos x + m x đồng biến trên ℝ
A. m ∈ ( - ∞ ; 13 ]
B. m ∈ [ - 13 ; + ∞ )
C. m ∈ [ 13 ; + ∞ )
D. m ∈ ( - ∞ ; - 13 ]
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx+ cosx+ mx đồng biến trên ℝ
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx + cosx + mx đồng biến trên ℝ
A. - 2 ≤ m ≤ 2
B. m ≤ - 2
C. - 2 < m < 2
D. m ≥ 2
Đáp án D
YCBT: y ' = cos x - sin x + m ≥ 0 với mọi x ∈ ℝ ⇔ m ≥ sin x - cos x = f x với x ∈ ℝ .
Mà ta có: f x = sin x - cos x = 2 x - π 4 ⇒ - 2 ≤ f x ≤ 2 ⇒ m ≥ 2
Tìm tất cả các giá trị của tham số m để hàm số f x = m 2 − 4 x 3 + 3 m − 2 x 2 + 3 x − 4 đồng biến trên ℝ .
A. m ≥ 2
B. m ≤ 2
C. m > 2
D. m < 2
Đáp án A
Với m = 2 ⇒ f x = 3 x − 4 ⇒ hàm số đồng biến trên ℝ .
Với m = − 2 ⇒ y = − 12 x 2 + 3 x − 4 ⇒ hàm số không đồng biến trên ℝ .
Với m ≠ ± 2 ⇒ f ' x = 3 m 2 − 4 x 2 + 6 m − 2 x + 3
Khi đó hàm số đồng biến trên ℝ ⇔ a = m 2 − 4 > 0 Δ ' = m − 2 2 − m 2 − 4 = − 4 m + 8 ≤ 0 ⇔ m > 2.
Kết hợp 3 trường hợp suy ra m ≥ 2 là giá trị cần tìm