Cho tam giác AOB vuông tại O, có O A B ^ = 30 0 và AB = a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = πa 2 2
B. S x q = πa 2
C. S x q = πa 2 4
D. S x q = 2 πa 2
Những câu hỏi liên quan
Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P
a) Giả sử (BCA) ̂=〖30〗^0. Tính số đo cung nhỏ và cung lớn AB, số đo (PAB) ̂ , số đo (AOB) ̂
b) Chứng minh
c) Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Chứng minh:
MB
a: sđ cung nhỏ AB=2*30=60 độ
sđ cung lớn AB là 360-60=300 độ
góc PAB=góc BCA=30 độ
góc AOB=sđ cung nhỏ AB=60 độ
b,c: Bạn ghi lại đề đi bạn
Đúng 0
Bình luận (0)
Cho tam giác AOB vuông tại O và OAB 30
°
. Đường cao hạ từ O là OH, OH a. Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA. A.
π
3
a
3
B.
9
10
π
a
3
C.
9
8
π
a
3
D.
8...
Đọc tiếp
Cho tam giác AOB vuông tại O và OAB = 30 ° . Đường cao hạ từ O là OH, OH = a. Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA.
A. π 3 a 3
B. 9 10 π a 3
C. 9 8 π a 3
D. 8 9 π a 3
Đáp án D
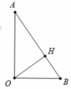
Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3
Đúng 0
Bình luận (0)
cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác AOB đồng dạng với tam giác ADB
b) Tính độ dài AD
c) CM : tam giác AOB đồng dạng với tam giác COD
d) Tính tỉ số diện tích của tam giác AOB và COD
Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P a) Giả sử (BCA) ̂=〖30〗^0. Tính số đo cung nhỏ và cung lớn AB, số đo (PAB) ̂ , số đo (AOB) ̂ b) Chứng minh c) Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Chứng minh: MB
Cho tam giác AOB vuông tại O, có
O
A
B
^
30
0
và AB a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh
S
x
q
của hình nón đó. A.
S
x
q...
Đọc tiếp
Cho tam giác AOB vuông tại O, có O A B ^ = 30 0 và AB = a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = π a 2 2 .
B. S x q = π a 2 .
C. S x q = π a 2 4 .
D. S x q = 2 π a 2 .
Đáp án A.
Bán kính đáy hình nón r = O B = A B sin 30 0 = a 2
Độ dài đường sinh l = A B = a ⇒ S x q = π r l = π a 2 2 .
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A lấy điểm O € tấm giác ABC sao cho gốc OBC =30*, góc OCB=15*. CMR các tam giác ABC và tam giác AOB cân
cho tam giác ABC vuông tại A có BC=2a; B = 300 và đường tròn (O) đường kính AB (như hình vẽ). Quay hình tròn (O) và tam giác ABC quanh cạnh AB cố định thì được một hình cầu và một hình nón. so sánh diện tích mặt cầu và diện tích toàn phần của hình nón
Cho tam giác ABC có phân giác BD; CE cắt tại O. Chứng minh:
a, BD vuông góc AC và CE vuông góc AB
b, OA=OB=OC
c,góc AOB=góc BOC= góc COA
84. Cho tam giác ABC vuông cân tại A. Điểm O ở trong tam giác sao cho \(\widehat{OBC}=30^o;\widehat{OCB}=15^o.\)Chứng minh các tam giác AOC, AOB cân.
vẽ tam giác đều BCM ( M và A cùng thuộc 1 nửa mặt phẳng bờ BC )
CM được tam giác COA cân tại C
\(\widehat{ACO}=45^o-15^o=30^o\)
\(\widehat{CAO}=\left(180^o-30^o\right):2=75^o\)
\(\widehat{BAO}=90^o-75^o=15^o\); \(\widehat{ABO}=45^o-30^o=15^o\)
Vậy \(\widehat{BAO}=\widehat{ABO}\)suy ra : \(\Delta AOB\)cân tại O
Đúng 0
Bình luận (0)
