Kí hiệu M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của M m .
A. 2
B. 2 3
C. 4 3
D. 5 3
Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y = x + 4 - x 2 . Khi đó
A. M - m = 2 2 - 2
B. M - m = 4
C. M - m = 2 2 + 2
D. M - m = 2 2
Kí hiệu M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của M m .
![]()
![]()
![]()
![]()
Kí hiệu M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của tỉ số M m .
A. 4 3
B. 6
C. 3
D. 3 2
Kí hiệu M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của tỉ số M m .
A. 4 3
B. 3
C. 1
D. 4
Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [0;3]. Tính giá trị của tỉ số M m
A. 4 3
B. 5 3
C. 2 3
D. 1 3
Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 3 2 x - 1 trên đoạn [1;4]. Tính giá trị biểu thức d = M – m
A. d = 3
B. d = 4
C. d = 5
D. d = 2
Đáp án A
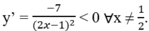
Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số nghịch biến trên đoạn [1; 4]. Vậy m = y(4) = 1; M = y(1) = 4 => d = M – m = 4 – 1 = 3
Kí hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn 0 ; 2 . Khi đó giá trị của a + A bằng:
A. 7
B. 18
C. 0
D. 12
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=sin2 x+2 sinx trên đoạn [0;3π/2]. Giá trị a+b bằng
A. 3 3 - 2 4
B. 3 3 + 2 2
C. 3 3 - 2 2
D. 3 3 - 4 2
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = x + 9 x trên đoạn [1;4]. Tính hiệu M - m.
A. M - m = 1 4
B. M - m = 15 4
C. M - m = 16
D. M - m = 4
Đáp án D
f ' x = 1 - 9 x 2 = x 2 - 9 x 2 = 0 → x ∈ 1 ; 4 x = 3 . So sánh các f 1 = 10 = M , f 3 = 6 = m , f 4 = 25 4 .
Vậy M - m = 10 - 6 = 4