Tính thể tích của khối lăng trụ đều ABC. A’B’C’ có AB = AA’ =a
A. 3 a 3 4
B. 3 a 3 6
C. a 3
D. 3 a 3 12
Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, biết AA = AB = AC =a. Tính thể tích khối lăng trụ ABC.A’B’C’
A. 3 a 3 4
B. a 3 2 4
C. a 3 3 4
D. a 3 4
Cho hình lăng trụ đứng ABC. A’B’C’ có tam giác ABC vuông tại A, AB= AA’=a, AC =2a . Tính thể tích khối lăng trụ đã cho
A. a 3 3
B. 2 a 3 3
C. a 3
D. 2 a 3
Cho hình lăng trụ tam giác đều ABC. A’B’C’ có AA'= a 3 Gọi I là giao điểm của AB’ và A’B. Cho biết khoảng cách từ I đến mặt phẳng (BCC'B') bằng a 3 2 . Tính thể tích khối lăng trụ ABC. A’B’C’.
A. 3 a 3
B. a 3
C. 3 a 3 4
D. a 3 4
Đáp án A
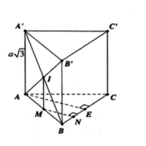
Gọi E là trung điểm BC, M là trung điểm của BE, M là trung điểm của AB.

Cho hình lăng trụ ABC. A’B’C’ có đáy là tam giác vuông cân tại A, AB =a. Biết thể tích của khối lăng trụ ABC. A’B’C’ là V = 4 a 3 3 Tính khoảng cách giữa hai đường thẳng AB và B’C’
A. h = 8 a 3
B. h = 3 a 8
C. h = 2 a 3
D. h = a 3
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, A A ' = 2 a . Một khối trục có hai đáy là hai hình tròn lần lượt nội tiếp tam giác ABC và tam giác A’B’C’. Tính thể tích V của khối trục đó.
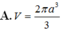
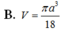
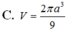
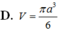
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Một khối trục có hai đáy là hai hình tròn lần lượt nội tiếp tam giác ABC và tam giác A’B’C’. Tính thể tích V của khối trục đó
A. V = 2 πa 3 3
B. V = πa 3 18
C. V = 2 πa 3 9
D. V = πa 3 6
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB=2a, AA'=a 3 . Tính thể tích khối lăng trụ ABC.A’B’C’
A. 3 a 3
B. a 3
C. a 3 4
D. 3 a 3 4
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=2a, AA'=a 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.
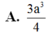
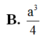
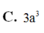
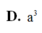
Cho hình lăng trụ đứng ABC.A’B’C’ có một đáy là tam giác ABC vuông tại A; AB = 3a,BC = 5a. Biết khối trụ có hai đáy là hai đường tròn nội tiếp hai tam giác ABC, A’B’C’ và có thể tích bằng 2 π a 3 . Chiều cao AA’ của lăng trụ bằng
A. 3a
B. 3 a
C. 2a
D. 2 a