Cho mặt cầu ( S 1 ) có bán kính R 1 , mặt cầu ( S 2 ) có bán kính R 2 = 2 R 1 . Tính tỉ số diện tích của mặt cầu ( S 1 ) và ( S 2 ) ?
A. 4.
B. 3.
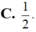
D. 2.
Vị trí tương đối của hai mặt cầu (S) có tâm I(1;1;1), bán kính R = 1 và mặt cầu (S’) có tâm I'(3;3;3), bán kính R’=1 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án A
![]()
Do đó, hai mặt cầu đã cho ở ngoài nhau.
Cho A 1 ; 1 ; 0 ; B - 1 ; 1 ; 0 ; C 1 ; - 1 ; 0 ; D - 1 ; - 1 ; 0 là tâm của 4 mặt cầu có bán kính bằng 1. Gọi I là tâm mặt cầu (S) có bán kính bằng 1 tiếp xúc ngoài với cả 4 mặt cầu kể trên. Tính bán kính R của mặt cầu ngoại tiếp hình chóp I.ABCD.
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng ( α ) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai?
A. R = r 2 + d 2 ( O , ( α ) )
B. d ( O , ( α ) ) < r
C. Diện tích của mặt cầu là S = 4 πr 2
D. Đường tròn lớn của mặt cầu có bán kính bằng bsn kính mặt cầu.
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng α cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai?
A. R = r 2 + d 2 O , α
B. d O , α < r
C. Diện tích của mặt cầu là S = 4 πr 2
D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu.
Trong không gian với hệ trục tọa độ Oxyz, cho các mặt cầu (S1), (S2), (S3) có bán kính r=1 và lần lượt có tâm là các điểm A(0;3;-1), B(-2;1;-1), C(4;-1;-1). Gọi (S) là mặt cầu tiếp xúc với cả ba mặt cầu trên. Mặt cầu (S) có bán kính nhỏ nhất là
![]()
![]()
![]()
![]()
Đáp án D.
Mặt cầu tiếp xúc với cả ba mặt cầu trên là mặt cầu tiếp xúc ngoài với cả 3 mặt cầu trên. Gọi I là tâm và R là bán kính mặt cầu cần tìm
Ta có:
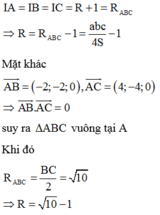
Trong không gian với hệ trục tọa độ Oxyz, cho các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) có bán kính r=1 và lần lượt có tâm là các điểm A(0;3;-1), B(-2;1;-1), C(4;-1;-1). Gọi (S) là mặt cầu tiếp xúc với cả ba mặt cầu trên. Mặt cầu (S) có bán kính nhỏ nhất là bao nhiêu?
A. R= 10
B. R= 10 - 1
C. R= 2 2 - 1
D. 2 2
Trong không gian Oxyz cho hai mặt phẳng P : x - y + 2 z + 1 = 0 và Q : 2 x + y + z - 1 = 0 . Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2, (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa mãn yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Chọn đáp án D
Giả sử mặt cầu (S) có tâm I m ; 0 ; 0 và bán kính là R (do I ∈ O x ).
Ta có
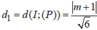
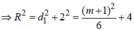
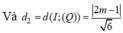
![]()
Từ đó suy ra
![]()
![]()
Để có đúng một mặt cầu (S) thỏa mãn yêu cầu khi và chỉ khi phương trình (*) có đúng một nghiệm m, tức là
![]()
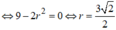
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Chọn D
Gọi I (m; 0; 0) là tâm mặt cầu có bán kính R, d1, d2 là các khoảng cách từ I đến (P) và (Q).
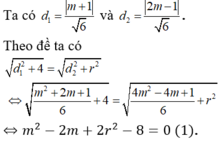
Yêu cầu bài toán tương đương phương trình (1) có đúng một nghiệm m
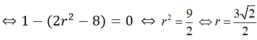
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 9
B. ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
C. x 2 + y 2 + z 2 - 2x - 4y + 2z - 3 = 0
D. x 2 + y 2 + z 2 = 9
Đáp án B
Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.
Phương trình mặt cầu (S’) là: ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
Trong không gian Oxyz cho các mặt phẳng P : x − y + 2 z + 1 = 0 , Q : 2 x + y + z − 1 = 0 Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3 .
B. r = 2 .
C. r = 3 2 .
D. r = 3 2 2 .
Đáp án D.
Gọi I a ; 0 ; 0 là tâm của mặt cầu (S) có bán kính R.
Khoảng cách từ tâm I đến hai mặt phẳng (P) và (Q) lần lượt là d 1 = a + 1 6 , d 2 = 2 a + 1 6
Theo giả thiết, ta có:
R 2 = d 1 2 + 2 2 = d 2 2 + r 2 ⇔ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a 2 + 2 a + 25 = 4 a 2 − 4 a + 1 + 6 r 2 ⇔ 3 a 2 − 6 a + 6 r 2 − 24 = 0 *
Yêu cầu bài toán (*) có nghiệm duy nhất
⇔ Δ ' = − 3 2 − 3 6 r 2 − 24 = 0 ⇔ r = 3 2 2 .