Đáp án D

Số phức biểu diễn điểm M có dạng a+bi

Có   (Do M là trung điểm của AB)

Chọn A

Đáp án B

Ta có  | 1   +   i |   =   ( 1   +   1 )   =   2 . Gọi M là điểm biểu diễn của z ta có |z| = OM.

Do đó:  | z |   =   | 1   +   i |   ⇔   O M   =   2 R =   2   .

Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính 

Chọn đáp án D.

Đặt z = a + bi (a, b ∈ R). Ta có:

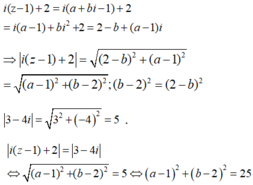
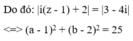
Tập hợp các điểm M(a,b) biểu diễn của số phức z là đường tròn tâm I(1;2), bán kính là R=5

Chọn A

Ta có: |   1   +   3 i |   =   ( 1   +   3 )   =   2 . Đặt z = a + bi(a, b ∈R). Ta có:

| z   +   i |   =   | 1   +   3 i |   <=> |a + (1 - b)i| = 2 <=>  a 2 + ( 1 - b ) 2 = 4

Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(0 ;1), bán kính R = 2

Chọn C