Đáp án A.

Đáp án C

Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:

Từ đó ta có:

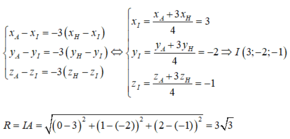
Vậy đáp án C đúng.

Gọi I là tâm của hình vuông thì I chính là hình chiếu của C lên BD

Ta có: I ( -1+4t;1-t;-1+t )nên  C I → = 4 t - 2 ; 2 - t ; t + 1

Vì C I ⊥ B D nên 

C I ⇀ . u B D → = 0 ⇔ 4 4 t - 2 - 2 - t + t + 1 = 0 ⇔ t = 1 2

Do đó:  I 1 ; 1 2 ; - 1 2 , C I - 3 2 2

I là trung điểm AC ⇒ A ( 1;2;3 )

Tọa độ điểm B - 1 + 4 t ; 1 - t ; - 1 + t  với  t > 1 4

Ta có IB = IC nên

- 2 + 4 t 2 + 1 2 - t 2 + 1 2 + t 2 = 9 2 ⇔ t 2 - t = 0 ⇔ t = 0 t = 1

Tọa độ điểm B ( 3;0;0 ). Suy ra d ( -1;1;-1 )

Đáp án D

Chọn A

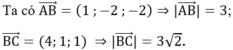
Theo giả thiết ABCD vuông tại A và B và có diện tích bằng 6√2 nên:

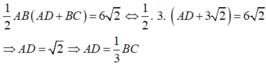
Do ABCD là hình thang vuông tại A và B nên . Giả sử  khi đó ta có:

Chọn D

Chọn B

Chọn D

Hình chiếu vuông góc của điểm A(-2;1;3) lên trục Ox là A(-2;0;0).

Chọn đáp án B.