Cho số phức z = a + bi thỏa z + 2iz = 3 + 3i. Tính giá trị của biểu thức P = a 2016 + b 2017
A. 0
B. 2
C. 3 4032 - 3 2017 5 2017
D. - 3 4032 - 3 2017 5 2017
Cho số phức z=a+bi,a,b thuộc R thỏa mãn z + 2 i z ¯ = 3 + 3 i . Tính giá trị biểu thức: P = ( a + i ) 2019 + ( b - i ) 2019
A.![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho số phức z=a+bi ( a , b ∈ R ) thỏa mãn z + 2 i z ¯ = 3 + 3 i . Tính z
A. z = 2
B. z = 5
C. z = 5
D. z = 2
Cho số phức z = a + bi thỏa mãn z + 2 i . z = 3 + 3 i Tính giá trị của biểu thức P = a 2017 + b 2018
A. 0
B. 2
C. 3 4034 - 3 2018 5 2018
D. - 3 4034 - 3 2018 5 2018
Gọi z = a + bi. Suy ra z = a - b i ⇒ i . z = i a + b
Khi đó
z + 2 i . z = a + b i + 2 i a + b = a + 2 b + b + 2 a i = 3 + 3 i ⇒ a + 2 b = 3 b + 2 a = 3 ⇒ a = b = 1
Do đó P = 1 2017 + 1 2018 = 2
Đáp án B
Xét các số phức z = a + bi, (a,b i) thỏa mãn |z – 3 – 3i| = 6. Tính P = 3a + b khi biểu thức 2|z + 6 – 3i| + |z + 1 + 5i| đạt giá trị nhỏ nhất.
A. P = 20
B. P = 2 + 20
C. P = - 20
D. P = - 2 - 20
Đáp án A
Phương pháp:
Cách giải:
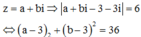
Khi đó ta có:
![]()
![]()
![]()
![]()
Xét các số phức z = a + b i a , b ∈ ℝ thỏa mãn điều kiện z − 4 − 3 i = 5. Tính P = a + b khi giá trị biểu thức z + 1 − 3 i + z − 1 + i đạt giá trị lớn nhất.
A. P = 10.
B. P = 4.
C. P = 6.
D. P = 8.
Đáp án A.
Gọi M x , y là điểm biểu diễn số phức z.
Từ giả thiết, ta có z − 4 − 3 i = 5 ⇔ x − 4 2 + y − 3 2 = 5 ⇒ M thuộc đường tròn (C) tâm I 4 ; 3 , bán kính R = 5 . Khi đó P = M A + M B , với A − 1 ; 3 , B 1 ; − 1 .
Ta có
P 2 = M A 2 + M B 2 + 2 M A . M B ≤ 2 M A 2 + M B 2 .
Gọi E 0 ; 1 là trung điểm của AB
⇒ M E 2 = M A 2 + M B 2 2 − A B 2 4 .
Do đó P 2 ≤ 4 M E 2 + A B 2 mà
M E ≤ C E = 3 5 s u y r a P 2 ≤ 4. 3 5 2 + 2 5 2 = 200.
Với C là giao điểm của đường thẳng EI
với đường tròn (C).
Vậy P ≤ 10 2 . Dấu “=” xảy ra
⇔ M A = M B M = C ⇒ M 6 ; 4 ⇒ a + b = 10.
Xét các số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn điều kiện |z - 4 - 3i| = 5 . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i + |z - 1 + i|| đạt giá trị lớn nhất.
A. P = 10
B. P = 4
D. P = 6
D. P = 8
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| =
5
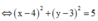
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có ![]()
Gọi E(0;1) là trung điểm của AB ![]()
Do đó ![]() mà
mà ![]() suy ra
suy ra ![]()
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy ![]() Dấu “=”xảy ra
Dấu “=”xảy ra 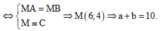
Xét các số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn điều kiện |z - 4 - 3i| = 5 . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i| + |z - 1 + i| đạt giá trị lớn nhất.
A. P = 10
B. P = 4
C. P = 6
D. P = 8
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có ![]()
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có
![]()
![]()
Gọi E(0;1) là trung điểm của AB
![]()
Do đó ![]() mà
mà ![]()
suy ra ![]()
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy ![]() Dấu “=” xảy ra
Dấu “=” xảy ra ![]()
=> a + b = 10
Xét các số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn điều kiện |z-4-3i| = 5 . Tính P = a + b khi giá trị biểu thức |z+1-3i| + |z-1+i| đạt giá trị lớn nhất.
A. P = 10
B. P = 4
C. P = 6
D. P = 8
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có ![]()
![]()
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =
5
. Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có: ![]()
![]()
Gọi E(0;1) là trung điểm của AB ![]()
Do đó ![]() mà
mà ![]() suy ra
suy ra ![]()
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy ![]() Dấu “=” xảy ra
Dấu “=” xảy ra 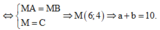
Cho số phức z = a+bi a , b ∈ R thoả mãn z - 2 i z - 2 là số thuần ảo. Khi số phức z có môđun lớn nhất. Tính giá trị biểu thức P=a+b
A. P = 0
B. P = 4
C. P = 2 2 + 1
D. P = 1 + 3 2