Cho hàm số y = 2 x 4 - 5 x 2 - 7 . Số tiếp tuyến đi qua điểm M(0; -7) của đồ thị hàm số là
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = x 3 - 3 x + 2 ( C ) . Tìm phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(-1; 0).
A. y = 0
B. y = x + 1
C. y = x - 1
D. y = 2
Hệ số góc của tiếp tuyến của đồ thị hàm số y = x - 1 x + 1 tại giao điểm của đồ thị hàm số với trục tung bằng
A. -2
B. 2
C. -1
D. 1
Giao điểm với trục tung B(0 ;-1). Ta có
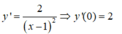
Hệ số góc của tiếp tuyến của đồ thị hàm số 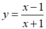 tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B
Cho hàm số 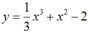 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là
có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là
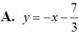
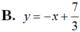
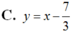
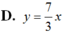
Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 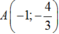 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.
Tìm hệ số góc tiếp tuyến của đồ thị hàm số y = − x 3 − 3 x 2 + 2 tại điểm có hoành độ là nghiêṃ của phương trình y ¢¢ = 0
A. 3
B. 2
C. 1
D. 4
Đáp án A
Hệ số góc của tiếp tuyến của đồ thị hàm số chính là đạo hàm cấp 1
Ta có y = − x 3 − 3 x 2 + 2 ⇒ y ' = − 3 x 2 − 6 x ⇒ y ' ' = − 6 x − 6
Phương trình y ' ' = 0 ⇔ x = − 1
Vậy hệ số góc cần tìm là k = y ' 1 = 3
Tiếp tuyến tại điểm A(0; 2) của đồ thị hàm số y = x 3 - 3 x + 2 có phương trình là
A. y = -3x + 2
B. y = 3x + 2
C. y = 2x + 2
D. y = x + 2
Tiếp tuyến tại điểm A(0; 2) của đồ thị hàm số y = x 3 - 3 x + 2 có phương trình là
A. y = -3x + 2
B. y = 3x + 2
C. y = 2x + 2
D. y = x + 2
Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y= x4-2x2+2
A.2
B.3
C.0
D.1
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
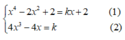
có nghiệm
Thay (2) vào (1) ta suy ra được
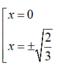
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
Qua điểm A(0;2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x 4 – 2 x 2 + 2 .
A. 2
B. 3
C. 0
D. 1
- Gọi d là tiếp tuyến của đồ thị hàm số đã cho qua A( 0, 2)
→ phương trình của d có dạng: y = k(x - 0) + 2 hay y = kx + 2
- Vì d tiếp xúc với đồ thị (C) nên hệ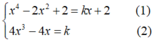 có nghiệm.
có nghiệm.
- Thay (2) vào (1) ta được :
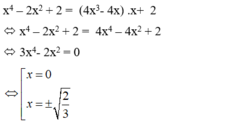
- Tương ứng với ba giá trị của x ta vừa tìm được, ta viết được 3 tiếp tuyến đi qua Ađến đồ thị (C).
Chọn B.
Cho hàm số y = 1 3 x 3 + x 2 - 2 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0 là:
A. y = - x - 7 3
B. y = - x + 7 3
C. y = x - 7 3
D. y = 7 3 x
Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
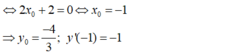
- Phương trình tiếp tuyến tại điểm 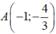 là:
là:
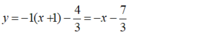
Chọn A.