Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
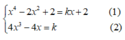
có nghiệm
Thay (2) vào (1) ta suy ra được
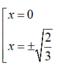
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
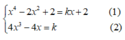
có nghiệm
Thay (2) vào (1) ta suy ra được
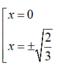
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
Tiếp tuyến tại điểm A(0; 2) của đồ thị hàm số y = x 3 - 3 x + 2 có phương trình là
A. y = -3x + 2
B. y = 3x + 2
C. y = 2x + 2
D. y = x + 2
Tiếp tuyến tại điểm A(0; 2) của đồ thị hàm số y = x 3 - 3 x + 2 có phương trình là
A. y = -3x + 2
B. y = 3x + 2
C. y = 2x + 2
D. y = x + 2
Hệ số góc của tiếp tuyến của đồ thị hàm số y = x - 1 x + 1 tại giao điểm của đồ thị hàm số với trục tung bằng
A. -2
B. 2
C. -1
D. 1
Cho hàm số y = 2 x 4 - 5 x 2 - 7 . Số tiếp tuyến đi qua điểm M(0; -7) của đồ thị hàm số là
A. 1
B. 2
C. 3
D. 4
Cho đồ thị hàm số y = x 3 - 2 x 2 + 2 x . Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016. Khi đó x 1 + x 2 bằng:
A. 4 3
B. - 4 3
C. 1 3
D. -1
Đồ thị của hàm số y = x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương?
A. 1
B. 2.
C. 3.
D. 4
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
![]()
![]()
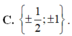
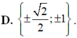
Cho hàm số y = x 3 - 3 x + 2 ( C ) . Tìm phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(-1; 0).
A. y = 0
B. y = x + 1
C. y = x - 1
D. y = 2
Số giao điểm của đồ thị hàm số y = x 3 - 3 x 2 + 2 x + 1 với trục hoành là
A. 0
B. 1
C. 2
D. 4