Hai điện tích q 1 = + q , q 2 = - q và đặt tại A và B trong không khí, biết AB = 2a. Tại M trên đường trung trực của AB thì E M có giá trị cực đại. Giá trị cực đại đó là
A. 8 k q 3 6 a 2
B. k q a 2
C. 2 k q a 2
D. 4 k q a 2
Hai điện tích q 1 = +q và q 2 = -q và đặt tại A và B trong không khí, biết AB = 2a. Tại M trên đường trung trực của AB thì E M có giá trị cực đại. Giá trị cực đại đó là
A. 8 k q 3 6 a 2
B. k q a 2
C. 2 k q a 2
D. 4 k q a 2
Chọn C
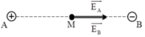
+ Dễ thấy rằng cường độ điện trường tổng hợp lớn nhất tại trung điểm của AB.
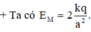
Hai điện tích điểm q 1 = 10 - 8 C đặt trong không khí tại hai điểm A và B cách nhau 8cm. Đặt trong điện tích điểm q = 10 - 8 C tại điểm M trên đường trung trực của đoạn AB và cách AB một khoảng 3cm. Lấy k = 9 . 10 9 N . m 2 / C 2 . Lực điện tổng hợp do q1 và q2 tác dụng lên q có độ lớn là
A. 1 , 23 . 10 - 3 N .
B. 1 , 34 . 10 - 3 N .
D. 1 , 04 . 10 - 3 N .
Hai điện tích q 1 = 3 . 10 - 8 C và q 2 = - 3 . 10 - 8 C đặt tại hai điểm A và B cách nhau một khoảng 6 cm trong không khí. Lực tác dụng lên điện tích q = 10 - 7 C đặt tại trung điểm O của AB là
A. 0 N
B. 0,09 N
C. 0,18 N
D. 0,06 N
Hai điện tích q 1 = 3.10 − 8 C và q 2 = − 3.10 − 8 C đặt tại hai điểm A và B cách nhau một khoảng 6 cm trong không khí. Lực tác dụng lên điện tích q = 10 − 7 C đặt tại trung điểm O của AB là
A. 0,18 N
B. 0,06 N
C. 0,09 N
D. 0 N
Hai điện tích điểm ![]() đặt trong không khí tại hai điểm A và B cách nhau 8cm. Đặt trong điện tích điểm
đặt trong không khí tại hai điểm A và B cách nhau 8cm. Đặt trong điện tích điểm ![]() tại điểm M trên đường trung trực của đoạn AB và cách AB một khoảng 3cm. Lấy
tại điểm M trên đường trung trực của đoạn AB và cách AB một khoảng 3cm. Lấy ![]() Lực điện tổng hợp do q1 và q2 tác dụng lên q có độ lớn là
Lực điện tổng hợp do q1 và q2 tác dụng lên q có độ lớn là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Hai điện tích điểm q 1 = 10 − 8 C v à q 2 = − 3.10 − 8 C đặt trong không khí tại hai điểm A và B cách nhau 8cm. Đặt điện tích điểm q = 10 − 8 C tại điểm M trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3cm. Lấy k = 9.10 9 N . m 2 / C 2 . Lực điện tổng hợp do q 1 và q 2 tác dụng lên q có độ lớn là
A. 1 , 23.10 − 3 N
B. 1 , 14.10 − 3 N
C. 1 , 44.10 − 3 N
D. 1 , 04.10 − 3 N
Hai điện tích điểm q 1 = 10 - 8 C và q 2 = - 3 . 10 - 8 C đặt trong không khí tại hai điểm A và B cách nhau 8 cm. Đặt điện tích điểm q= 10 - 8 tại điểm trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3 cm. Lấy k = 9 . 10 9 N . m 2 / C 2 . Lực điện tổng hợp do q 1 và q 2 tác dụng lên q có độ lớn là:
A. 1 , 23 . 10 - 3 N
B. 1 , 14 . 10 - 3 N
C. 1 , 44 . 10 - 3 N
D. 1 , 04 . 10 - 3 N
2 điện tích q1=2.10-8C , q2=-8.10-8C đặt tại A,B trong không khí (AB=8cm) . 1 điện tích q3 đặt tại C . hỏi :
a) điểm C ở đâu để q cân bằng ?
b) dấu và độ lớn của q3 để q1 và q2 cũng cân bằng ?
a) \(\dfrac{2}{x^2}=\dfrac{8}{\left(0.08+x\right)^2}\)
=> x= 0.08 (m ) => Q3 đặt cách Q1= 0.08m cách Q2= 0.16m
b) \(\dfrac{\left|q1.q3\right|}{0.08^2}=\dfrac{\left|q1.q2\right|}{0.08^2}\)
=> q1=q2=-8.10^-8C
2 điện tích q1=2.10-8C , q2=-8.10-8C đặt tại A,B trong không khí (AB=8cm) . 1 điện tích q3 đặt tại C . hỏi :
a) điểm C ở đâu để q cân bằng ?
b) dấu và độ lớn của q3 để q1 và q2 cũng cân bằng ?
a) vì \(q_1\) và \(q_2\) trái dấu nên \(q_3\) không thể đặc ở giữa \(AB\) và cũng không thể nằm ngoài giá của \(\overrightarrow{AB}\) vì khi đó tổng các lực tác dụng lên \(q_3\) sẽ khác không .
theo định luật \(Cu-lông\) ta có :
\(F_{13}=\dfrac{k.\left|q_1q_3\right|}{\varepsilon AC^2}=\dfrac{k\left|2.10^{-8}q_3\right|}{\varepsilon AC^2}\) ; \(F_{23}=\dfrac{k\left|q_2q_3\right|}{\varepsilon BC^2}=\dfrac{k\left|-8.10^{-8}q_3\right|}{\varepsilon BC^2}=\dfrac{k\left|8.10^{-8}q_3\right|}{\varepsilon BC^2}\)
\(\)để \(q_3\) cân bằng thì \(F_{13}=F_{23}\Leftrightarrow\dfrac{k\left|2.10^{-8}q_3\right|}{\varepsilon AC^2}=\dfrac{k\left|8.10^{-8}q_3\right|}{\varepsilon BC^2}\)
\(\Leftrightarrow\dfrac{AC^2}{BC^2}=\dfrac{2.10^{-8}}{8.10^{-8}}=\dfrac{1}{4}\Leftrightarrow\dfrac{AC}{BC}=\dfrac{1}{2}\Leftrightarrow BC=2AC\)
\(\Rightarrow A\) là trung điểm của \(BC\) với đoạn \(AB=8cm\) .
b) theo nhận xét ta thấy \(q_3< 0\) vì nếu \(q_3>0\) thì \(F_{31}\) cùng hướng với \(F_{21}\) nên \(q_1\) không thể nào cân bằng
để \(q_1\) và \(q_2\) cần bằng thì : \(\left\{{}\begin{matrix}F_{31}=F_{21}\\F_{32}=F_{12}\end{matrix}\right.\Leftrightarrow F_{31}=F_{21}=F_{32}\)
nên ta chỉ cần \(F_{31}=F_{21}\) là đủ
\(\Rightarrow\dfrac{K\left|q_3q_1\right|}{\varepsilon AC^2}=\dfrac{k\left|q_2q_1\right|}{\varepsilon AB^2}\Leftrightarrow\dfrac{k\left|q_3q_1\right|}{\varepsilon8^2}=\dfrac{k\left|q_2q_1\right|}{\varepsilon8^2}\Leftrightarrow\left|q_3\right|=\left|q_2\right|\)
\(\Leftrightarrow\left|q_3\right|=\left|-8.10^{-8}\right|=8.10^{-8}\Leftrightarrow q_3=\pm8.10^{-8}\)
mà \(q_3< 0\Rightarrow q_3=-8.10^{-8}\)
vậy \(q_3=-8.10^{-8}\)