Tìm các số phức 2z + z ¯ và 25 i z biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
Cho số phức z thỏa mãn z - 2 + i z ¯ - 2 - i = 25 . Biết tập hợp các điểm M biểu diễn số phức w = 2 z ¯ - 2 + 3 i là đường tròn có tâm I(a;b) và bán kính c. Giá trị của a+b+c bằng
A. 17
B. 20
C. 10
D. 18
Cho số phức z thỏa mãn z − 2 + i z ¯ − 2 − i = 25 . Biết tập hợp các điểm M biểu diễn số phức w = 2 z ¯ − 2 + 3 i là đường tròn tâm I a ; b và bán kính c. Giá trị của a + b + c bằng
A. 10
B. 18
C. 17
D. 20

Ta có:
A 2 ; − 1 Đ O x ⇁ B 2 ; 1 V O 0 ; 0 ; k = 2 ⇁ C 4 ; 2 T u → − 2 ; 3 ⇁ D 2 ; 5

Cho số phức z , biết 2 z - 1 1 + i + z ¯ + 1 1 - i = 2 - 2 i . Tìm số phức liên hợp của số phức w = 3 z - 3 i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Cho số phức z biết z + 2 z ¯ = 1 - i 2 1 + i 2 2 - i (1).
Tìm tổng phần thực và phần ảo của z
A. 4 2 - 2 15
B. - 2 2 - 4 5
C. - 2 2 - 14 15
D. - 2 2 - 14 5
Tìm số phức z biết rằng z + 2 z ¯ = 3 - i
A. z = 1 + i
B. z = 1 - 1 3 i
C. z = - 1 + i
D. z = - 1 - i
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
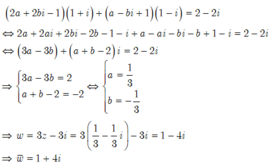
Tìm số phức z thỏa mãn 2 z − i = z − z ¯ + 2 i và z ¯ + i = 2 i 100
A. z = 2 + i ; z = 2 − i
B. z=−2+i;z=2+i
C. z = − 2 + i ; z = 1 + 2 i
D. z = − 2 + i ; z = 2 + i ; − 3 + 2 3 i ; − 3 − 2 3 i
Tìm các số phức 2z +
z
và 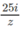 biết rằng z = 3 – 4i
biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
2z + z = 2(3 − 4i) + 3 + 4i = 6 − 8i + 3 + 4i = 9 − 4i
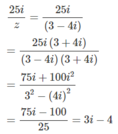
Tìm mô đun của số phức z biết 2 z - 1 1 + i + z ¯ ‐ 1 1 - i = 2 - 2 i .
A. 1 9
B. 2 3
C. 2 9
D. 1 3