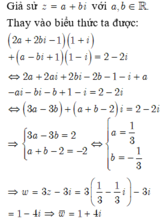Các câu hỏi tương tự
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
+
z
)
z
¯
. A. -2 B. 0. C. -...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho các số phức z và w thỏa mãn
(
3
-
i
)
z
z
w
-
1
+
1
-
i
.
Tìm GTLN của
T
w
+
i
.
A.
2
2
B. ...
Đọc tiếp
Cho các số phức z và w thỏa mãn ( 3 - i ) z = z w - 1 + 1 - i . Tìm GTLN của T = w + i .
A. 2 2
B. 3 2 2
C. 2
D. 1 2
Cho số phức z2+3i. Module số phức
w
(
3
-
2
z
¯
)
(
z
+
1
)
-
i
là A.
3
15
B.
7
13
C.
6
7
D.
123
Đọc tiếp
Cho số phức z=2+3i. Module số phức w = ( 3 - 2 z ¯ ) ( z + 1 ) - i là
A. 3 15
B. 7 13
C. 6 7
D. 123
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w=(3-4i)z-1+2i là đường tròn tâm I, bán kính R. Tìm tọa độ tâm I và bán kính R của đường tròn đó
A. I(1;2); R= 5
B. I(1;-2); R=5
C. I(1;2); R=5
D. I(-1;2); R=5
Cho số phức z thỏa mãn |z|1. Biết tập hợp các điểm biểu diễn số phức w(3-4i)z-1+2i là đường tròn tâm I, bán kính R. Tìm tọa đọ tâm I và bán kính R của đường tròn đó. A. I(-1; 2); R
5
B. I(1; 2); R 5 C. I(1; 2); R
5
D. I(-1; 2); R 5
Đọc tiếp
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w=(3-4i)z-1+2i là đường tròn tâm I, bán kính R. Tìm tọa đọ tâm I và bán kính R của đường tròn đó.
A. I(-1; 2); R = 5
B. I(1; 2); R = 5
C. I(1; 2); R = 5
D. I(-1; 2); R = 5
Cho số phức z thỏa mãn
z
-
3
+
4
i
2
và w 2z + 1 – i. Trong mặt phẳng phức, tập hợp điểm biểu diễn số phức w là đường tròn tâm I, bán kính R . Khi đó: A. I (-7;9), R 16 B. I (-7;9), R 4 C. I (7;-9), R 16 D. I (7;-9), R 4.
Đọc tiếp
Cho số phức z thỏa mãn z - 3 + 4 i = 2 và w = 2z + 1 – i. Trong mặt phẳng phức, tập hợp điểm biểu diễn số phức w là đường tròn tâm I, bán kính R . Khi đó:
A. I (-7;9), R = 16
B. I (-7;9), R = 4
C. I (7;-9), R = 16
D. I (7;-9), R = 4.
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Cho số phức z thỏa mãn tập hợp
z
-
1
3
. Biết rằng tập hợp các điểm biểu diễn số phức w với
3
-
2
i
w
i
z
+
2
là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó. A.
I
8
13
;
1...
Đọc tiếp
Cho số phức z thỏa mãn tập hợp z - 1 = 3 . Biết rằng tập hợp các điểm biểu diễn số phức w với 3 - 2 i w = i z + 2 là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó.
A. I 8 13 ; 1 13 , r = 3 13
B. I - 2 ; 3 , r = 13
C. I 4 13 ; 7 13 , r = 3 13
D. I 2 3 ; - 1 2 , r = 3
Cho số phức z thỏa mãn tập hợp
z
-
1
3
. Biết rằng tập hợp các điểm biểu diễn số phức w với
3
-
2
i
w
i
z
+
2
là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó. A.
I
8
13
;
1...
Đọc tiếp
Cho số phức z thỏa mãn tập hợp z - 1 = 3 . Biết rằng tập hợp các điểm biểu diễn số phức w với 3 - 2 i w = i z + 2 là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó.
A. I 8 13 ; 1 13 , r = 3 13
B. I - 2 ; 3 , r = 13
C. I 4 13 ; 7 13 , r = 3 13
D. I 2 3 ; - 1 2 , r = 3
Tìm mô đun của số phức
w
z
3
+
z
+
1
z
2
+
1
biết rằng số phức z thỏa mãn điều kiện
z
+
z
1
+...
Đọc tiếp
Tìm mô đun của số phức w = z 3 + z + 1 z 2 + 1 biết rằng số phức z thỏa mãn điều kiện z + z 1 + i + z - z 2 + 3 i = 4 - i
A. 170 10
B. 171 10
C. 172 10
D. 173 10