Chứng minh hai tia phân giác của hai góc kề bù vuông góc với nhau

Những câu hỏi liên quan
Chứng minh rằng:
a)Hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau.
b)Hai tia phân giác của hai góc kề bù thì vuông góc với nhau
chứng minh định lí : hai tia phân giác của hai góc kề bù vuông góc với nhau
1. Chứng minh rằng tia phân giác của hai góc kề bù thì vuông góc với nhau.
2. Cho góc xOy và góc yOz là hai góc kề bù. Tia Om là phân giác của góc xOy. Trên cùng một nửa mp bờ xz chứa tia Oy, vẽ tia On sao cho: On vuông góc với Om. Chứng minh rằng : tia On là tia phân giác của góc yOz
1,Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
=> Đpcm
2,
Ta có:
( gt )
Mà ( Om là tia phân giác góc xOy )
On là tia phân giác góc yOz.
(A) Hai tia phân giác của cặp góc kề nhau thì vuông góc với nhau.
(B) Hai tia phân giác của cặp góc bù nhau thì vuông góc với nhau.
(C) Hai tia phân giác của cặp góc đối đỉnh thì vuông góc với nhau.
(D) Hai tia phân giác của cặp góc kề bù nhau thì vuông góc với nhau.
Chứng minh rằng hai tia phân giác của hai góc kề bù thì vuông góc với nhau
góc tù thua góc nhọn ,góc nhọn thua góc vuông ,góc vuông thua góc bẹt, góc bẹt góc thua góc bè góc bè thua góc nhọn
Đúng 0
Bình luận (0)
Gọi xOy và yOz là hai góc kề bù.Ot là phân giác của xOy, Ot' là phân giác của yOz
Ta có:
yOt =1/2 xOy( ot phân giác) (1)
yOt'=1/2 yOx ( ot' phân giác) (2)
xOy+ yOz = 180o( kề bù)
Từ (1) và (2) => yOt+ yOt'=1/2(xOy+yOz)=1/2.180=90o
=>tOt' =90o hay Ot vuông góc với Ot'
=> ĐPCM
Đúng 0
Bình luận (0)
Gọi xOy và yOz là hai góc kề bù.Ot là phân giác của xOy,
Ot' là phân giác của yOz
Ta có: yOt =1/2 xOy( ot phân giác) (1) y
Ot'=1/2 yOx ( ot' phân giác) (2)
xOy+ yOz = 180o( kề bù)
Từ (1) và (2) =
> yOt+ yOt'=1/2(xOy+yOz)=1/2.180=90o =>tOt' =90o hay Ot vuông góc với Ot' => ĐPCM
Đúng 0
Bình luận (0)
Chứng minh định lí: Hai tia phân giác của hai góc kề bù vuông góc với nhau.
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
Xin lỗi nha tớ ngại đánh máy lắm( mà cũng không biết giải nữa)
Đúng 1
Bình luận (0)
Bài 8*: Chứng minh rằng hai tia phân giác của hai góc kề bù thì vuông góc với nhau.
CẢm tạ !!
..........................
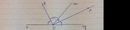



chứng minh hai tia phân giác của 2 góc kề bù thì vuông góc với nhau
Gọi AOC và COB là hai góc kề bù , OM và ON theo thứ tự là các tia phân giác của hai góc ấy . Ta có :
\(\widehat{MOC}+\widehat{CON}=\frac{\widehat{AOC}}{2}+\frac{\widehat{COB}}{2}=\frac{\widehat{AOC}+\widehat{COB}}{2}=\frac{180^0}{2}=90^0\)
Ta thấy tia OC nằm giữa hai tia OM và ON nên \(\widehat{MOC}+\widehat{CON}=\widehat{MON}\)
Do đó MON = 900 . Vậy \(OM\perp ON\)
Đúng 0
Bình luận (0)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
chứng minh hai tia phân giác của 2 góc kề bù thì vuông góc với nhau
trong sgk toán 7 bài định lý hình học có giải nhaa
- tập 1
Đúng 0
Bình luận (0)
Gọi hai góc kề bù là góc xOz và góc zOy.
On là tia phân giác góc xOz
Om là tia phân giác góc zOy.
Vì On là tia phân giác góc xOz
=> Góc zOn = \(\frac{1}{2}\widehat{xOz}\)( tính chất tia phân giác ) ( 1 )
Vì Om là tia phân giác góc zOy
=> \(\widehat{zOm}=\frac{1}{2}\widehat{zOy}\)( tính chất tia phân giác ) ( 2 )
Cộng vế với vế của (1), (2)
=> \(\widehat{nOz}+\widehat{zOm}=\frac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)
=> \(\widehat{nOm}=\frac{1}{2}\widehat{xOy}=\frac{180^o}{2}=90^o\)
=> Om vuông góc với On ( Hai tia phân giác của hai góc kề bù vuông góc với nhau )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
























