Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 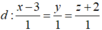 và điểm M(2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
và điểm M(2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?
A. 2.
B. 1.
C. 0.
D. Vô số.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng d : x = - 1 + t y = 2 + 2 t z = 1 - 2 t . Xác định tọa độ điểm M' là điểm đối xứng với M qua đường thẳng d.
A. M ' - 11 9 ; 14 9 ; - 1 9
B. M ' 31 9 ; - 10 9 ; 1 9
C. M ' - 31 9 ; 10 9 ; - 1 9
D. M ' - 11 9 ; 14 9 ; 13 9
Đáp án C
Gọi H là hình chiếu của M trên d
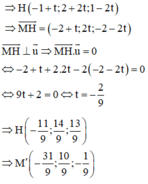
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M’ đối xứng với M qua d.
A. M'(3;-3;0)
B. M'(1;-3;2)
C. M'(0;-3;3)
D. M'(-1;-2;0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng d: x = - 1 + t y = 2 + 2 t z = 1 - 2 t . Xác định tọa độ điểm là điểm đối xứng với M qua đường thẳng d.
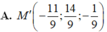
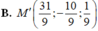
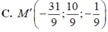
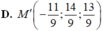
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; − 3 ; 1 và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M' đối xứng với M qua d.
A. M ' 3 ; − 3 ; 0 .
B. M ' 1 ; − 3 ; 2 .
C. M ' 0 ; − 3 ; 3 .
D. M ' − 1 ; − 2 ; 0 .
Đáp án C
d : x = − 1 + 2 t y = − 2 − t , t ∈ ℝ z = 2 t .
Gọi H là hình chiếu của M trên d ⇒ H − 1 + 2 t ; − 2 − t ; 2 t .
⇒ M H → = − 3 + 2 t ; 1 − t ; − 1 + 2 t
Ta có − 3 + 2 t .2 + 1 − t . − 1 + − 1 + 2 t .2 = 0 ⇔ t = 1 ⇒ H 1 ; − 3 ; 2
Suy ra M ' 0 ; − 3 ; 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x = t - 2 y = 2 + 3 t z = 1 + t . Đường thẳng d đi qua điểm M và có vectơ chỉ phương α d → có tọa độ là:
A. M(-2;2;1), α d → = - 1 ; 3 ; 1
B. M(1;2;1), α d → = - 2 ; 3 ; 1
C. M(2;-2;-1), α d → = 1 ; 3 ; 1
D. M(1;2;1), α d → = 2 ; - 3 ; 1
Chọn A.
Đường thẳng d đi qua M(-2;2;1) và có vectơ chỉ phương 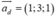
Trong không gian với hệ tọa độ Oxyz, cho điểm M ( 1;-3;2 ) và đường thẳng ∆ có phương trình x - 1 1 = y 2 = z - 2 1 . Tọa độ hình chiếu vuông góc của điểm M trên đường thẳng ∆ là
A. ( 0;-2;1 )
B. ( -1;1;-1 )
C. ( 1;0;2 )
D. ( 2;2;3 )
Gọi H 1 + t ; 2 t ; 2 + t ∈ ∆ là hình chiếu vuông góc của M trên đường thẳng ∆ .
Ta có M H → 1 + t ; 2 t ; 2 + t và u ∆ → 1 ; 2 ; 1 là VTCP của đường thẳng ∆
Vì
M H ⊥ ∆ ⇔ M H → . u ∆ → = 0 ⇔ t + 2 2 t + 3 + t = 0 ⇔ 6 t + 6 = 0 ⇔ t = - 1
nên H ( 0;-2;1 )
Chọn đáp án A
Trong không gian với hệ tọa độ Oxyz, cho điểm M 1 ; - 3 ; 2 và đường thẳng ∆ có phương trình x - 1 1 = y 2 = z - 2 1 . Tọa độ hình chiếu vuông góc của điểm M trên đường thẳng ∆ là
A. 0 ; - 2 ; 1
B. - 1 ; 1 ; - 1
C. 1 ; 0 ; 2
D. 2 ; 2 ; 3
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng 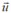 . Véc-tơ chỉ phương
. Véc-tơ chỉ phương ![]() của d và điểm M thuộc đường thẳng d là:
của d và điểm M thuộc đường thẳng d là:
A. ![]() =(6;-2;8),M(3;-1;4)
=(6;-2;8),M(3;-1;4)
B. ![]() =(2;3;-5),M(3;-1;4)
=(2;3;-5),M(3;-1;4)
C. ![]() =(3;-1;4),M(1;3;-4)
=(3;-1;4),M(1;3;-4)
D. ![]() =(6;-2;8),M(2;3;-5).
=(6;-2;8),M(2;3;-5).
Đáp án D
Ta có ![]() =(6;-2;8)=2(3;-1;4),M(2;3;-5).
=(6;-2;8)=2(3;-1;4),M(2;3;-5).
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z = 3 - t , d ' : x = 2 - 2 t ' y = - 2 + t ' z = 1 + 3 t ' . Tìm tọa độ giao điểm M của hai đường thẳng d và d’
A. M(-1;0;4)
B. M(4;0;-1)
C. M(0;4;-1)
D. M(0;-1;4)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(0;5;-3) và đường thẳng d : x = t y = 3 − t z = 2 . Tổng tọa độ điểm M’ là hình chiếu song song của M trên (Oxz) theo phương d là:
A. 2
B. 3
C. 4
D. 5
Đáp án A
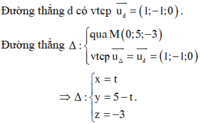
Em có M’ là hình chiếu song song của M trên (Oxz) ⇒ M ' = Δ ∩ Oxz ⇒ M ' 5 ; 0 ; − 3 .
Vậy tổng tọa độ của điểm M’ là 2.