Tìm phân thức Q thỏa mãn điều kiện: 2 a − 6 a 3 − 3 a 2 − a + 3 + Q = 6 a − 3 − 2 a 2 1 − a 2 , với a ≠ ± 1 và a ≠ 3 .

Những câu hỏi liên quan
cho biểu thức A=3/n+2 với n là số nguyên
a, số nguyên n phải thỏa mãn điều kiện gì để a là phân số
b, số nguyên n phải thỏa mãn điều kiện gì để a là số nguyên
c, tìm phân số A biết n=1, n=2, n=-7
A=3 phần n trừ 3 nhá em
tìm phân số có dạng a/48 thỏa mãn điều kiện 1/6<a/48<1/3 tìm phân số
9/48; 10/48; 11/48; 12/48; 13/48; 14/48; 15/48
Đúng 0
Bình luận (0)
\(\frac{1}{6}=\frac{8}{48}\)
\(\frac{1}{3}=\frac{12}{48}\)
Vậy \(\frac{8}{48}< \frac{9}{48};\frac{10}{48};\frac{11}{48}< \frac{12}{48}\)
Vậy a bằng 9;10;11
Đúng 0
Bình luận (0)
\(\frac{1}{6}< \frac{a}{48}< \frac{1}{3}\)
\(=\frac{8}{48}< \frac{a}{48}< \frac{16}{48}\)
\(=\frac{a}{48}=\frac{9}{48};\frac{10}{48};\frac{11}{48};\frac{12}{48};\frac{13}{48};\frac{14}{48};\frac{15}{48}\)
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện:
2
x
-
6
x
3
-
3
x
2
-
x
+
3
+
Q
6
x
-...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện: 2 x - 6 x 3 - 3 x 2 - x + 3 + Q = 6 x - 3 - 2 x 2 1 - x 2
Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện :
a) \(\dfrac{1}{x^2+x+1}-Q=\dfrac{1}{x-x^2}+\dfrac{x^2+2x}{x^3-1}\)
b) \(\dfrac{2x-6}{x^3-3x^2-x+3}+Q=\dfrac{6}{x-3}-\dfrac{2x^2}{1-x^2}\)
Cho biểu thức A=\(\frac{3}{n+2}\)với n là số nguyên
a) số nguyên n phải thỏa mãn điều kiện gì để A là phân số ?
b) Tìm phân số A biết n=0 n=2 n=-7
ae giúp mình
a) Để A là phân số thì
\(n+2\ne0=>n\ne-2\)2
b) Zới n=0 (TMĐK) thì biểu phân A là
\(\frac{3}{n+2}=>\frac{3}{0+2}=\frac{3}{2}\)
zậy phân số A là \(\frac{3}{2}\)khi n=0
mấy cái kia tương tự
bạn làm hết hộ mình mình còn bận học anh
Để A là phân số thì \(A\ne\frac{3}{0}\)
\(\Rightarrow n+2\ne0\)
\(\Rightarrow n\ne0-2\)
\(\Rightarrow n\ne2\)
Vậy để A là phân số thì \(n\ne2\)
b) Thay n = 0 vào phân số A, ta được:
\(A=\frac{3}{0+2}\)
\(A=\frac{3}{2}\)
Vậy giá trị của phân số A khi n = 0 là\(\frac{3}{2}\).
Thay n = 2 vào phân số A, ta được:
\(A=\frac{3}{2+2}\)
\(A=\frac{3}{4}\)
Vậy giá trị của phân số A khi n = 2 là \(\frac{3}{4}\).
Thay n = -7 vào phân số A, ta được:
\(A=\frac{3}{-7+2}\)
\(A=\frac{3}{-5}\)
Vậy giá trị của phân số A khi n = -7 là \(\frac{3}{-5}\)
Chúc bạn học tốt !!!
1 Tìm giá trị nhỏ nhất của bểu thức Cfrac{6}{left|xright|-3} với x là số nguyên2 . Tìm giá trị lớn nhất của biểu thức x-|x|3 . Tìm các số a và b thỏa mãn một điều trong các điều kiện sau :a ) a+b |a| + |b|b ) a+b |b| - |a|4 . Có bao nhiêu cặp số nguyên (x;y) thỏa mãn một trong các điều kiện sau :a ) |x| + |y| 20b) |x| + |y| 20( Các cặp số (3;4) và (4;3) là 2 cặp số khác nhau )
Đọc tiếp
1 Tìm giá trị nhỏ nhất của bểu thức \(C=\frac{6}{\left|x\right|-3}\) với x là số nguyên
2 . Tìm giá trị lớn nhất của biểu thức x-|x|
3 . Tìm các số a và b thỏa mãn một điều trong các điều kiện sau :
a ) a+b = |a| + |b|
b ) a+b = |b| - |a|
4 . Có bao nhiêu cặp số nguyên (x;y) thỏa mãn một trong các điều kiện sau :
a ) |x| + |y| = 20
b) |x| + |y| <20
( Các cặp số (3;4) và (4;3) là 2 cặp số khác nhau )
1)
Xét \(\left|x\right|>3\)\(\Rightarrow\)\(C>0\)
Xét \(0\le\left|x\right|< 3\)\(\Rightarrow\)\(C< 0\)
+ Với \(\left|x\right|=0\)\(\Leftrightarrow\)\(x=0\) thì \(C=-2\)
+ Với \(\left|x\right|=1\)\(\Leftrightarrow\)\(x=\pm1\) thì \(C=-3\)
+ Với \(\left|x\right|=2\)\(\Leftrightarrow\)\(x=\pm2\) thì \(C=-6\)
Vậy GTNN của \(C=-6\) khi \(x=\pm2\)
2)
Xét \(x\ge0\)\(\Rightarrow\)\(x-\left|x\right|=0\)
Xét \(x< 0\)\(\Rightarrow\)\(x-\left|x\right|=2x< 0\)
Vậy GTLN của \(x-\left|x\right|=0\) khi \(x>0\)
Ví dụ một bài toán :
Tìm GTLN của B = 10-4 | x-2|
Vì |x-2| \(\ge0\forall x\)
\(\Rightarrow-4.\left|x-2\right|\le0\forall x\). Tại sao mà tìm GTLN mà lại nhỏ hơn hoặc bằng 0 ạ
Còn một bài : Tìm GTNN của biểu thức A=2|3x-1| -4
Vì |3x-1| \(\ge0\)
\(\Rightarrow2\left|3x-1\right|\ge0\forall x\) cái này là timg GTNN mà giờ lại lớn hơ hoặc bằng 0 ạ
Xem thêm câu trả lời
Cho biểu thức A=3/n+2 với n là số nguyên
a) số nguyên n phải thỏa mãn điều kiện gì để A là phân số ?
b) Tìm phân số A biết n=0 n=2 n=-7
c) Tìm các số nguyên n để A là một số nguyên
Ta có: \(A=\dfrac{3}{n+2}\left(\forall n\in Z\right)\)
a) Để \(A\) là phân số thì \(n+2\ne0\Leftrightarrow n\ne-2\)
Vậy \(n\ne-2\) thì \(A\) là phân số.
b) Thay \(n=0;n=2;n=-7\) lần lượt vào \(A\) ta có:
\(\left\{{}\begin{matrix}A=\dfrac{3}{0+2}=\dfrac{3}{2}\\A=\dfrac{3}{2+2}=\dfrac{3}{4}\\A=\dfrac{3}{-7+2}=\dfrac{-3}{5}\end{matrix}\right.\)
c) Để \(A\in Z\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-1;-3;1;-5\right\}\)
Vậy \(n\in\left\{-1;-3;1;-5\right\}\) thì \(A\in Z\)
Đúng 3
Bình luận (0)
Cho hai số thực a,b thay đổi thỏa mãn điều kiện\(a+b\ge1\) và \(a>0\). Tìm giá trị nhỏ nhất của biểu thức: \(A=\frac{8a^2+b}{4a}+b^2\)
Cho a,b,c là các số dương thỏa mãn điều kiện: \(5a^2+2abc+4b^2+3c^2=60\) Tìm GTLN của biểu thức: \(A=a+b+c\)
Cho biểu thức A = 6/n-3 với n là số nguyên.
a.Số nguyên n phải thỏa mãn điều kiện gì để A là phân số.
b.Tìm các số nguyên n để AϵZ
a, Để A là phân số thì \(n-3\ne0\Rightarrow n\ne3\)
b, Để \(A\in Z\)
\(\Rightarrow\dfrac{6}{n-3}\in Z\\ \Rightarrow n-3\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
Ta có bảng
| n-3 | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| n | -3 | 0 | 1 | 2 | 4 | 5 | 6 | 9 |
Vậy \(n\in\left\{-3;0;1;2;4;5;6;9\right\}\)
Đúng 2
Bình luận (0)










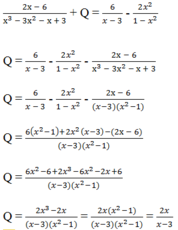




![Phạm minh ( {[ ae 2k6 ]}](https://hoc24.vn/images/avt/avt3144147_256by256.jpg)










