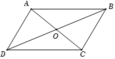
Gọi O là tâm hình bình hành ABCD; hai điểm E; F lần lượt là trung điểm AB; BC. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình bình hành ABCD. Trên các cạnh AB; BC; CD; DA lấy các điểm E; F; G; H sao cho AE = CG; BF = DH. CMR:
a, Xác định tâm đối xứng của hình bình hành ABCD
b, EFGH là hình bình hành và tìm tâm đối xứng
c, Gọi O là giao điểm của AC và BD, O còn là tâm đối xứng của hình bình hành nào?
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
![]()
![]()
![]()
![]()
Chọn B.
+ Đáp án A. Ta có ![]() . Vậy A đúng.
. Vậy A đúng.
+ Đáp án B. Ta có 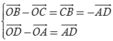 . Vậy B sai.
. Vậy B sai.
+ Đáp án C. Ta có ![]() .Vậy C đúng.
.Vậy C đúng.
+ Đáp án D. Ta có 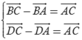 . Vậy D đúng.
. Vậy D đúng.
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. O A → − O B → = C D → .
B. O B → − O C → = O D → − O A → .
C. A B → − A D → = D B → .
D. B C → − B A → = D C → − D A → .
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm OB, OD
a) Chứng minh AMCN là hình bình hành
b) Hình bình hành ABCD cần có thêm điều kiện gì để AMCN là hình chữ nhật
c) AN cắt CD tại E, CM cắt AB tại tâm O. Chứng minh rằng E và F đối xứng với nhau qua tâm O
Cho hình bình hành ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và AD. Phép đối xứng tâm O biến.
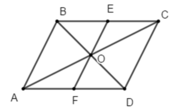
A. D F → thành E B ⇀
B. E C → thành A F →
C. B O → thành O D →
D. B E → thành D F →
ba phương án A, B, C đều sai về hướng của vecto
Đáp án D
Cho hình chóp S.ABCD có ABCD là hình bình hành tâm O. Gọi K là trung điểm của SC. Chứng minh rằng : KO // ( SAB).
Lời giải:
Vì $ABCD$ là hình bình hành nên tâm $O$ là trung điểm $AC$
$\Rightarrow OK$ là đường trung bình của $SAC$ ứng với cạnh $SA$
$\Rightarrow OK\parallel SA$
Mà $SA\subset (SAB)$ nên $OK\parallel (SAB)$
Cho hình bình hành S.ABCD có đáy là ABCD là hình bình hành tâm O Gọi M N Q lần lượt trên SA SB SD Tìm giao điểm của đường thẳng SC và mặt phẳng mnq