Cho hàm số y = 2 x 3 - 3 x 2 – 5 . Các nghiệm của phương trình y’ = 0 là
A. x = ± 1
B. x = - 1 ∪ x = 5 2
C. x = - 5 2 ∪ x = 1
D. x = 0 ∪ x = 1
1/ cho hệ phương trình:
\(\orbr{\begin{cases}nx-y=2\\3x+ny=5\end{cases}}\)
a/ tìm nghiệm (x;y) của hệ theo n
b/ vs giá trị nào của n thì hệ có nghiệm (x;y) thỏa mãn: x + y = 1 - \(\frac{n^2}{n^2+3}\)
2/ a/ gọi 2 nghiệm của phương trình x2 - 7x - 11 =0 là x1 và x2. Hãy lập 1 phương trình bậc hai có các nghiệm là x1 + x2 và x1x2
b/ cho pt bậc hai( ẩn x): x2 - (2m+1)x + m2 + m - 6=0. Tìm m để pt có 2 nghiệm đều là số dương
c/ cho hàm số y= 3mx - 3(m+1). Vs giá trị nào của m thì đồ thị hàm số đi qua điểm (2;-6). Vẽ đồ thị hàm số ứng vs giá trị m vừa tìm đc
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số y = f (x) có bảng biến thiên như sau
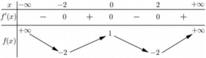
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số y = f (x) có bảng biến thiên như sau
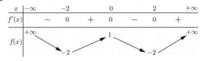
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Đáp án A
Phương pháp:
+) Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m.
+) Dựa vào BBT để xác định số giao điểm của các đồ thị hàm số.
Cách giải:
Ta có: ![]()
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = - 3 2
Dựa vào BBT ta thấy đường thẳng y = - 3 2 cắt đồ thị hàm số y = f(x) tại 4 điểm phân biệt
=>Phương trình có 4 nghiệm phân biệt
Cho hàm số y = ( 2 m + 2 ) x 2 . Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình: x − y = 1 2 x − y = 3
A. m = 7 4
B. m = 1 4
C. m = 7 8
D. m = - 7 8
1) Vẽ đồ thị của hàm số $y=-2 x^{2}$.
2) Cho phương trình $x^{2}+(1-m) x-m=0$ (với $x$ là ẩn số, $m$ là tham số). Xác định các giá trị của $m$ để phương trình có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn điều kiện $x_{1}\left(5-x_{2}\right) \geq 5\left(3-x_{2}\right)-36$.
Bài 1 : Ta có : x 0 0
y 0 0
bài 1 là mình đặt x = 0 rồi y = 0 nhé, đặt số nào cũng được nha nhưng mình chọn số 0 vì nó dễ :v nên mn đừng thắc mắc nhá
Bài 2 :
Để pt có 2 nghiệm pb nên \(\Delta>0\)hay
\(\left(1-m\right)^2-4\left(-m\right)=m^2-2m+1+4m=\left(m+1\right)^2>0\)
\(\Leftrightarrow m>-1\)
Theo Vi et \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=m-1\\x_1x_2=\frac{c}{a}=-m\end{cases}}\)
Ta có : \(x_1\left(5-x_2\right)\ge5\left(3-x_2\right)-36\Leftrightarrow5x_1-x_1x_2\ge15-5x_2-36\)
\(\Leftrightarrow5\left(x_1+x_2\right)-x_1x_2\ge-21\Leftrightarrow5m-5+m\ge-21\)
\(\Leftrightarrow6m\ge-16\Leftrightarrow m\ge-\frac{8}{3}\)kết hợp với đk vậy \(m>-1\)
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2|f(x)| - 5 = 0 là
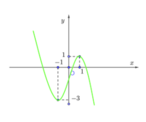
A. 3
B.5
C. 4
D. 6
Cho hàm số \(y=\dfrac{1}{4}x^3-\dfrac{3}{2}x^2+5\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho
b) Tìm các giá trị của tham số m để phương trình \(x^3-6x^2+m=0\) có 3 nghiệm phân biệt
Bài 1:cho phương trình x^2 - 6x + m=0. Với giá trị nào của m thì phương trình có 2 nghiệm trái dấu
Bài 2 :cho phương trình x^2 + 2 (m+1) x + m^2=0. Tìm m để phương trinh co 2 nghiem phan biet, trong đó có 1 nghiệm bằng -2
Bài 3:cho pt x^2 -(m+5) x + m - 6=0. Tìm m để pt có 1 nghiệm bằng -2. Tim nghiệm còn lại
Bài 4:cho hàm số y=-2x^2 có đồ thị là parabol (P) và hàm số y==4x + m. Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ âm
Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên a ; b và f a . f b < 0 thì tồn tại x 0 ∈ a ; b sao cho f x 0 = 0.
2. Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm duy nhất trên ( a ; b ) .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai
B. Cả ba mệnh đề đều đúng
C. Cả ba mệnh đề đều sai
D. Có đúng một mệnh đề sai
Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG