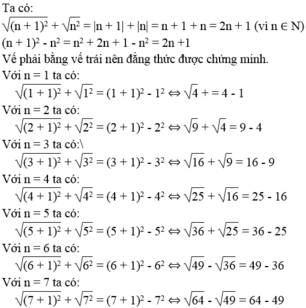Chứng minh phân thức 7 n - 5 3 n - 2 là tối giản với mọi số tự nhiên n

Những câu hỏi liên quan
a) Cho biểu thức A=3/2+n n khác -2 Tìm các số nguyên n để A là một số nguyên.
b) Chứng minh phân số n+6/n=7 là phân số tối giản với mọi số n nguyên và n khác -7 .
a: Để A nguyên thì \(n+2\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{-1;-3;1;-5\right\}\)
b: n+6/n+7
Gọi d=ƯCLN(n+6;n+7)
=>n+6-n-7 chiahết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG
Đúng 3
Bình luận (0)
a) Phân tích đa thức sau thành nhân tử: x^3(x^2-7)^2-36x
b) Cho biểu thức: A=n^3(n^2-7)^2-36n
Chứng minh Achia hết cho 5040 với mọi số tự nhiên n
Với n là số tự nhiên, chứng minh đẳng thức:
n
+
1
2
+
n
2
n
+
1
2...
Đọc tiếp
Với n là số tự nhiên, chứng minh đẳng thức:
n + 1 2 + n 2 = n + 1 2 - n 2
Viết đẳng thức trên khi n là 1, 2, 3, 4, 5, 6, 7
Chứng minh rằng các phân số sau tối giản
a) \(\dfrac{2n+7}{2n+3}\) (n ∈ N)
b)\(\dfrac{6n+5}{8n+7}\)(n ∈ N)
c)\(\dfrac{2^{2024}+3}{2^{2023}+1}\) tối giản
a: Gọi d=ƯCLN(2n+7;2n+3)
=>2n+7 chia hết cho d và 2n+3 chia hết cho d
=>2n+7-2n-3 chia hết cho d
=>4 chia hết cho d
mà 2n+7 lẻ
nên d=1
=>PSTG
b: Gọi d=ƯCLN(6n+5;8n+7)
=>4(6n+5)-3(8n+7) chia hết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG
Đúng 0
Bình luận (0)
Chứng minh phân thức 2 n + 5 3 n + 7 là tối giản với mọi số tự nhiên n
Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 5 và 3n + 7
⇒ (2n + 5)⋮ d và (3n + 7)⋮ d
⇒ [3(2n + 5) - 2(3n + 7)] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 0
Bình luận (0)
Chứng minh rằng n7+n2+1/n8+n+1 chưa phải là phân thức tối giản
a) Phân tích đa thức sau thành nhân tử: \(x^3\left(x^2-7\right)^2-36x\)
b)Cho biểu thức: \(A=n^3\cdot\left(n^2-7\right)^2-36n\)
Chứng minh rằng A chia hết cho 5040 với mọi số tự nhiên n
b) Phân tích ra thừa số : 5040 = 24 . 32 . 5 . 7
Phân tích : A = n . [ n2 . ( n2 - 7 )2 - 36 ] = n . [ ( n3 - 7n )2 - 62 ]
= n . ( n3 - 7n - 6 ) . ( n3 - 7n + 6 )
Ta lại có : n3 - 7n - 6 = ( n + 1 ) ( n + 2 ) ( n - 3 )
n3 - 7n + 6 = ( n - 1 ) ( n - 2 ) ( n + 3 )
Do đó : A = ( n - 3 ) ( n - 2 ) ( n - 1 ) n ( n + 1 ) ( n + 2 ) ( n + 3 )
Ta thấy A là tích của 7 số nguyên liên tiếp nên :
- tồn tại 1 bội số của 5 ( nên A chia hết cho 5 )
- tồn tại 1 bội số của 7 ( nên A chia hết cho 7 )
- tồn tại 2 bội số của 3 ( nên A chia hết cho 9 )
- tồn tại 3 bội số của 2, trong đó có 1 bội số của 4 ( nên A chia hết cho 16 )
A chia hết cho các số 5,7,9,16 đôi một nguyên tố cùng nhau nên A chia hết cho 5.7.9.16 = 5040
Đúng 0
Bình luận (0)
1) Tìm số nguyên n để phân số sau có giá trị là số nguyên: a) -5/n-2 (viết dưới dạng phân số) b) n-5/n+1 (phân số) c)3n-7/n+1 (phân số)2) Chứng minh với mọi số nguyên n các phân số sau tối giản: a) 2n+1/2n+2 (phân số) b) 2n+5/2n+3 (phân số)3) Cho M1.2.3.....2004.(1+1/2+1/3+...+1/2004). Chứng minh: M chia hết cho 5.4) Tìm số nguyên a và b sao cho: a/9-1/bb1/3.
Đọc tiếp
1) Tìm số nguyên n để phân số sau có giá trị là số nguyên:
a) -5/n-2 (viết dưới dạng phân số) b) n-5/n+1 (phân số) c)3n-7/n+1 (phân số)
2) Chứng minh với mọi số nguyên n các phân số sau tối giản:
a) 2n+1/2n+2 (phân số) b) 2n+5/2n+3 (phân số)
3) Cho M=1.2.3.....2004.(1+1/2+1/3+...+1/2004). Chứng minh: M chia hết cho 5.
4) Tìm số nguyên a và b sao cho: a/9-1/bb=1/3.
Cho f(n)= n5 - 5. n3 + 4 n với n nguyên
a> Phân tích đa thức thành nhân tử.
b> Chứng minh f(n) chia hết cho 120 với mọi n ≥ 2
xem ở đây nè:
http://d.violet.vn//uploads/resources/733/3687956/preview.swf
bài 1 nhé
Đúng 0
Bình luận (0)
Chứng minh rằng phân thức A = \(\dfrac{n+3}{n+2}\) tối giản
Tính giá trị của biểu thức A tại x = -2
ĐK:n≠-2
Gọi \(d=ƯCLN\left(n+3,n+2\right)\)
\(\Rightarrow n+3⋮d;n+2⋮d\\ \Rightarrow n+3-n-2⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\)
Vậy n+3 và n+2 nctn hay \(\dfrac{n+3}{n+2}\) tối giản
Với n=-2 trái vs ĐKXĐ nên A ko xác định
Đúng 2
Bình luận (0)