Nếu số phức z ≠ 1 thỏa mãn z = 1 thì phần thực của số phức 1 1 − z bằng
A. 1
B. − 1 2
C. 1 2
D. 2
Nếu số phức z≠1 thỏa mãn |z|=1 thì phần thực của số phức 1 1 - z bằng
A. 1
B. 2
C. -1/2
D. 1/2
Cho số phức z thỏa mãn z = 2 z ¯ + 1 + 3 i . Phần thực của số phức z là
A. -3
B. -1
C. 1
D. 2
Cho số phức z thỏa mãn (1+2i)z=6-3i Phần thực của số phức z là:
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn 1 + 2 i z = 6 − 3 i . Phần thực của số phức z là:
A. -3
B. 3
C. 0
D. -3i
Chọn C.
Phương pháp:
Giải phương trình phức cơ bản tìm số phức z .
Cách giải:

Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
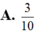
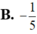
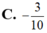
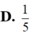
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng:
A. 3 10
B. - 1 5
C. - 3 10
C. 1 5
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z = - 7 + 3 i + z . Môđun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Gọi z=a+bi a ∈ ℝ , b ∈ ℝ , ta có:
![]()
![]()
![]()
![]()
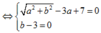
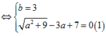
Giải (1) ta có:
![]()
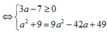
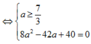
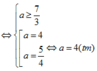
Do đó a=4; b=3; ⇒ z=4+3i
Khi đó
![]()
=1-4-3i+16+24i-9=4-21i
Vậy w = 4 2 + - 21 2 = 457 .
Chọn đáp án D.
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z - z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457