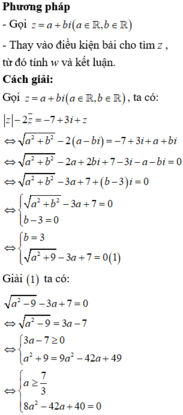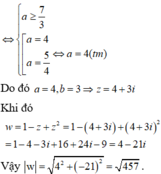Các câu hỏi tương tự
Cho số phức z có phần thực là số nguyên và z thỏa mãn
z
-
2
z
¯
-
7
+
3
i
+
z
. Mô đun của số phức
w
1
-
z
+
z
2
bằng A.
w
445
B.
w
42...
Đọc tiếp
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho các số phức z, w khác 0 và thỏa mãn |z-w| 2|z| |w|. Phẩn thực của số phức
u
z
w
là: A.
a
1
4
B. a 1 C.
a
1
8
D.
a
-
1
8
Đọc tiếp
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho số phức z thỏa mãn
z
−
1
−
i
1
, số phức w thỏa mãn
w
¯
−
2
−
3
i
2
. Tìm giá trị nhỏ nhất của
z
−
w
....
Đọc tiếp
Cho số phức z thỏa mãn z − 1 − i = 1 , số phức w thỏa mãn w ¯ − 2 − 3 i = 2 . Tìm giá trị nhỏ nhất của z − w .
A. 17 + 3
B. 13 + 3
C. 13 - 3
D. 17 - 3
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tính giá trị nhỏ nhất của
z
-
w...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Số phức thỏa mãn phương trình
z
+
3
z
2
+
i
3
(
2
-
i
)
Mô đun của số phức w z + 10i là A.
15
4
B.
1521
4
C.
5
73...
Đọc tiếp
Số phức thỏa mãn phương trình z + 3 z = 2 + i 3 ( 2 - i ) Mô đun của số phức w = z + 10i là
A. 15 4
B. 1521 4
C. 5 73 4
D. 4
Cho hai số phức z,w thỏa mãn z+3w
2
+
2
3
i
và |z-w|2. Giá trị lớn nhất của biểu thức P|z|+|w| bằng A.
2
21
B.
2
7
C.
21
3
D.
2
21
3
Đọc tiếp
Cho hai số phức z,w thỏa mãn z+3w= 2 + 2 3 i và |z-w|=2. Giá trị lớn nhất của biểu thức P=|z|+|w| bằng
A. 2 21
B. 2 7
C. 21 3
D. 2 21 3
Tìm mô đun của số phức
w
z
3
+
z
+
1
z
2
+
1
biết rằng số phức z thỏa mãn điều kiện
z
+
z
1
+...
Đọc tiếp
Tìm mô đun của số phức w = z 3 + z + 1 z 2 + 1 biết rằng số phức z thỏa mãn điều kiện z + z 1 + i + z - z 2 + 3 i = 4 - i
A. 170 10
B. 171 10
C. 172 10
D. 173 10
Cho số phức z thỏa mãn |z| 5 và số phức
w
(
1
+
i
)
z
Tìm |w| A.
10
B.
2
+
5
C. 5 D.
2
5
Đọc tiếp
Cho số phức z thỏa mãn |z| = 5 và số phức w = ( 1 + i ) z Tìm |w|
A. 10
B. 2 + 5
C. 5
D. 2 5
Cho số phức z thỏa mãn
2
+
i
z
+
2
1
+
2
i
1
+
i
7
+
8
i
. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức
w...
Đọc tiếp
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính P = a 2 + b 2
A. P = 5
B. P = 7
C. P = 13
D. P = 25