cho hs y= x3/3-2x2+3x+2/3 tọa độ điểm cực đjai của đt hàm số là

Những câu hỏi liên quan
Cho hàm số y x3/3 – 2x2 + 3x + 2/3. Toạ độ điểm cực đại của đồ thị hàm số là A. (-1;2) B. (3;2/3). C. (1;-2) D. (1;2)
Đọc tiếp
Cho hàm số y = x3/3 – 2x2 + 3x + 2/3. Toạ độ điểm cực đại của đồ thị hàm số là
A. (-1;2)
B. (3;2/3).
C. (1;-2)
D. (1;2)
Đáp án D.
Tập xác định D = R.
Ta có y’ = x2 – 4x + 3, y’ = 0
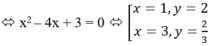
Bảng biến thiên
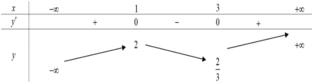
Tọa độ điểm cực đại của hàm số là (1;2).
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
x
3
-
2
x
2
+
x
+
3
có tọa độ điểm cực tiểu là A. (3;1) B. (-1;-1) C.
1
3
;
85...
Đọc tiếp
Đồ thị hàm số y = x 3 - 2 x 2 + x + 3 có tọa độ điểm cực tiểu là
A. (3;1)
B. (-1;-1)
C. 1 3 ; 85 27
D. (1;3)
Chọn D
+ T a c ó : y ' = 3 x 2 - 4 x + 1
![]()
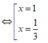
Hàm số đạt cực tiểu tại x = 1 ⇒ y C T = 3
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
+
2
. Tọa độ điểm cực tiểu của đồ thị hàm số là
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 . Tọa độ điểm cực tiểu của đồ thị hàm số là
![]()
![]()
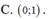
![]()
Cho hàm số y = x 3 - 3 x + 2 . Tọa độ điểm cực tiểu của đồ thị hàm số là
A. (-2;0)
B. (-1;4)
C. (0;1)
D. (1;0)
Đáp án D
Ta có y ' = 3 x 2 - 3 ⇒ y ' ' = 6 x , y ' = 0 ⇔ x = ± 1 → y ' ' 1 > 0 y ' ' - 1 < 0 ⇒ hàm số đạt cực tiểu tại x = 1. ⇒ Điểm cực tiểu A(1;0)
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
+
2
. Tọa độ điểm cực tiểu của đồ thị hàm số là A. (
-
2;0) B. (
-
1;4) C. (0;1) D. (1;0)
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 . Tọa độ điểm cực tiểu của đồ thị hàm số là
A. ( - 2;0)
B. ( - 1;4)
C. (0;1)
D. (1;0)
Đáp án D
Ta có
![]()
Mặt khác
![]()
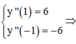
Tọa độ cực tiểu của đồ thị hàm số là (1;0)
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
3
-
2
x
2
+
3
x
+
2
3
. Tọa độ điểm cực tiểu của đồ thị hàm số là B. (1; -2) C. (1; 2) D. (-1; 2)
Đọc tiếp
Cho hàm số y = x 3 3 - 2 x 2 + 3 x + 2 3 . Tọa độ điểm cực tiểu của đồ thị hàm số là
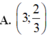
B. (1; -2)
C. (1; 2)
D. (-1; 2)
Cho hàm số
y
x
3
3
-
2
x
2
+
3
x
+
2
3
. Tọa độ điểm cực đại của đồ thị hàm số là A. (-1;2) B. (1;2) C. (1;-2) D.
3
;
2
3
Đọc tiếp
Cho hàm số y = x 3 3 - 2 x 2 + 3 x + 2 3 . Tọa độ điểm cực đại của đồ thị hàm số là
A. (-1;2)
B. (1;2)
C. (1;-2)
D. 3 ; 2 3
Chọn B.
Do đó hàm số có cực đại là (1;2), cực tiểu là 3 ; 2 3 .
Đúng 0
Bình luận (0)
Cho các hàm số sau:
y
1
x
−
3
I
;
y
x
3
−
3
x
+
2
I
I
;
y
−
x
4
+
2
x
2
...
Đọc tiếp
Cho các hàm số sau:
y = 1 x − 3 I ; y = x 3 − 3 x + 2 I I ; y = − x 4 + 2 x 2 I I I .
Trong các hàm số đã cho hàm không có cực trị là:
A. Chỉ (II)
B. Chỉ (III)
C. Chỉ (I)
D. (I) và (II)
Đáp án là C
• Hàm số (I) là hàm nhất biến nên không có cực trị.
• Hàm số (II) có phương trình y'=2 có 2 nghiệm phân biệt nên có 2 cực trị.
Hàm số (III) có a.b=-2<0 nên có 3 cực trị.
Đúng 0
Bình luận (0)
Gọi
x
1
là điểm cực đại,
x
2
là điểm cực tiểu của hàm số
y
-
x
3
+
3
x
+
2
. Giá trị của biểu thức
S
x
1
+
2
x
2
bằng A. -1 B. 0 C. 1 D. 2
Đọc tiếp
Gọi x 1 là điểm cực đại, x 2 là điểm cực tiểu của hàm số y = - x 3 + 3 x + 2 . Giá trị của biểu thức S = x 1 + 2 x 2 bằng
A. -1
B. 0
C. 1
D. 2
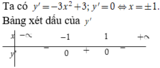
Từ đó suy ra hàm số đạt cực tiểu tại x 1 = 1, đạt cực đại tại x 2 = -1
Suy ra S = x 1 + 2 x 2 = -1
Chọn A.
Đúng 0
Bình luận (0)




