Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z - 4 i + z + 4 i = 10
A. Một đường tròn
B. Một elip
C. Một hypebol
D. Một parabol
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
A. Đường tròn I - 1 ; 0 , bán kính R = 4
B. Đường tròn I 1 ; 0 , bán kính R = 2
C. Hình tròn tâm I 1 ; 0 , bán kính R = 2
D. Hình tròn tâm I - 1 ; 0 , bán kính R = 2
Đáp án D
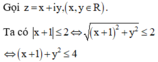
Vậy tập hợp điểm M biểu diễn số phức z thỏa mãn điều kiện đầu bài là hình tròn tâm I(-1;0), bán kính R = 2
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
![]()
![]()
![]()
D. Hình tròn tâm I (-1;0) Bán kính R = 2
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
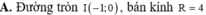
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
A. Đường tròn I − 1 ; 0 , bán kính R=4
B. Đường tròn I 1 ; 0 , bán kính R=4
C. Đường tròn I 1 ; 0 , bán kính R=2
D. Đường tròn I − 1 ; 0 , bán kính R=2
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: z ¯ + 1 − i ≤ 4
A. Đường tròn tâm I (-1; -1) , bán kính R = 4.
B. Hình tròn tâm I (1; -1), bán kính R = 4.
C. Hình tròn tâm I (-1; -1), bán kính R = 4 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I (1; -1), bán kính R = 4.
Trên mặt phẳng Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện 1 ≤ z - 2 i < 2
A. Hình tròn tâm I ( 0;2 ) và bán kính R = 2
B. Hình tròn tâm I ( 0;2 )và bán kính R = 1
C. Hình tròn tâm I ( 0;2 ) và bán kính R = 1 đồng thời trừ đi phần trong của hình tròn tâm I ( 0;2 ) bán kính R' = 1
D. Hình tròn tâm I ( 0;2 ) và bán kính R = 1 đồng thời trừ đi hình tròn tâm I ( 0;2 ) bán kính R' = 1
Gọi z = a + bi với a , b ∈ R
Ta có 1 ≤ z - 2 i < 2 ⇔ 1 ≤ a 2 + b - 2 2 < 4
Vậy tập hợp các điểm M là hình tròn tâm I ( 0;2 ) và bán kính R = 2 đồng thời trừ đi hình tròn tâm I ( 0;2 ) bán kính R' = 1 . (Chúng ta thường nhầm lẫn giữa hai đáp án C và D )
Đáp án D
Xét các số phức z thỏa mãn điều kiện |z-3+2i|=5. Trong mặt phẳng tọa độ Oxy, tập hợp của điểm biểu diễn số phức z là
A.Đường tròn tâmI(3;-2),bán kính R=5
B.Đường tròn tâm I(-2;1), bán kính R=5
C.Đường tròn tâm I(4;-3),bán kính R=5.
D. Đường tròn tâm I(-4;3), bán kính R=5
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: | z + i | = | z - i | .
A. Trục Oy.
B. Trục Ox.
C. y = x.
D. y = -x.
Chọn B.
Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi trong mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có
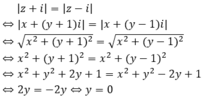
Vậy tập hợp các điểm M là đường thẳng y = 0 hay trục Ox