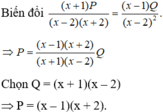Tìm phân thức Q thỏa mãn đẳng thức sau: Q : 4 q 2 − 4 2 q + 3 = 4 q 2 + 12 q + 9 q − 1 với q ≠ − 3 2 và q ≠ 1

Những câu hỏi liên quan
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức :
x
+
2
P
x
-
2
x
-
1
Q
x
2...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức : x + 2 P x - 2 = x - 1 Q x 2 - 4
x + 2 P x - 2 = x - 1 Q x 2 - 4
⇒ x + 2 . P . x 2 - 4 = x - 2 x - 1 . Q
Hay (x + 2)(x – 2)(x + 2).P = (x – 2)(x – 1).Q
Chọn P = (x – 1) thì Q = x + 2 2
Đúng 0
Bình luận (0)
Tìm một cặp đa thức P và Q thỏa mãn đẳng thức:
(
x
+
1
)
P
x
2
−
4
(
x
−
1
)
Q
x
2...
Đọc tiếp
Tìm một cặp đa thức P và Q thỏa mãn đẳng thức:
( x + 1 ) P x 2 − 4 = ( x − 1 ) Q x 2 − 4 x + 4 với x ≠ ± 2 .
tìm x thuộc Q thỏa mãn lần lượt các đẳng thức sau
(x+\(\frac{3}{5}\)) . (\(\frac{-4}{3}\)-x)=0
\(\left(x+\frac{3}{5}\right).\left(\frac{-4}{3}-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{3}{5}=0\\\frac{-4}{3}-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-3}{5}\\x=\frac{-4}{3}\end{cases}}}\)
Đúng 0
Bình luận (0)
\(\left(x+\frac{3}{5}\right)\left(-\frac{4}{3}-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+\frac{3}{5}=0\\-\frac{4}{3}-x=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-\frac{3}{5}\\x=-\frac{4}{3}\end{cases}}}\)
vậy \(x=-\frac{3}{5}\)hoặc \(x=-\frac{4}{3}\).
Đúng 0
Bình luận (0)
ta có : \(\left(x+\frac{3}{5}\right)\left(-\frac{4}{3}-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{3}{5}=0\\\frac{-4}{3}-x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{3}{5}\\x=-\frac{4}{3}\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm đa thức Q;P thỏa mãn đẳng thức
\(\frac{\left(x+2\right)\cdot P}{x-2}=\frac{\left(x-1\right)\cdot Q}{x^2-4}\)
điều kiện \(x\ne2;x\ne-2\)
\(\frac{\left(x+2\right)^2.P}{x^2-4}=\frac{\left(x-1\right).Q}{x^2-4}\)
\(\left(x+2\right)^2.P=\left(x-1\right)Q\)
\(P=x-1\)
\(Q=\left(x+2\right)^2\)
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức:
x
+
2
.
P
x
2
-
1
x
-
2
.
Q...
Đọc tiếp
Trong mỗi trường hợp sau hãy tìm hai đa thức P và Q thỏa mãn đẳng thức: x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1
x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1
⇒ x + 2 . P . x 2 - 2 x + 1 = x 2 - 1 x - 2 . Q
Hay x + 2 x - 1 2 . P = x - 1 x + 1 x - 2 . Q
Chọn P = (x – 2)(x + 1) = x 2 - x - 2 thì Q = (x + 2)(x – 1) = x 2 + x - 2
Đúng 0
Bình luận (0)
Tìm phân thức T thỏa mãn đẳng thức sau:
1
x
.
x
x
+
2
.
x
+
2
x
+
4
.
.
..
.
x
+
14...
Đọc tiếp
Tìm phân thức T thỏa mãn đẳng thức sau: 1 x . x x + 2 . x + 2 x + 4 . . .. . x + 14 x + 16 . x + 16 x + 18 . x + 18 x + 20 . T = 1 2 , với các mẫu thỏa mãn x ≠ 0
Biến đổi ta được: 1 x + 20 . T = 1 2 ⇒ T = x + 20 2
Đúng 0
Bình luận (0)
Trong mỗi trường hợp sau đây, hãy tìm hai đa thức P và Q thỏa mãn đẳng thức :
a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
b) \(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
\(\Leftrightarrow\left(x^2-4\right)\left(x+2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2\left(x-2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2P=\left(x-1\right)Q\)
\(\Leftrightarrow P=x-1\)
\(Q=\left(x+2\right)^2=x^2+4x+4\)
b)\(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)P=\left(x+1\right)\left(x-1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)P=\left(x+1\right)\left(x-2\right)Q\)
\(\Leftrightarrow P=\left(x+1\right)\left(x-2\right)=x^2-x-2\)
\(Q=\left(x-1\right)\left(x+2\right)=x^2+x-2\)
Đúng 0
Bình luận (0)
Cho \(x,y\)là các số thực thỏa mãn đẳng thức \(\left(x+2\right)\left(y+2\right)=\frac{25}{4}\)
Tìm giá trị nhỏ nhất của biểu thức \(F=\sqrt{1+x^4}+\sqrt{1+y^4}\)
Hì , giải đc rùi nha.
Vì \(x,y\in R\)
\(\Rightarrow\left(x+2\right).\left(y+2\right)=\frac{25}{4}\)
Min \(P=\sqrt{1+x^4}+\sqrt{1+y^4}\)
- Dự đoán \(x=y=\frac{1}{2}\)
- Sử dụng BĐT : \(\frac{x^2}{a}+\frac{y^2}{b}\ge\frac{\left(x+y\right)^2}{a+b}\) ( Với a,b > 0 )
=> \(1+x^4=16.\frac{1}{16}+a^4=16.\left(\frac{1}{4}\right)^2+a^2\ge\frac{[16.\frac{1}{4}+a^2]^2}{17}\)
\(=\frac{(a^2+4)^2}{17}\)
=> \(1+y^4\ge\frac{\left(y^2+4\right)^2}{17}\)
=> \(P\ge\frac{x^2+y^2+8}{\sqrt{17}}\)
\(\Leftrightarrow P\sqrt{17}=\frac{1}{5}\left(x^2+y^2\right)+\frac{4}{5}\left(x^2+\frac{1}{4}+y^2+\frac{1}{4}\right)+8-\frac{2}{5}\)
\(\ge\frac{2xy}{5}+\frac{4}{5}\left(x+y\right)+8-\frac{2}{5}=\frac{2}{5}[xy+2\left(x+y\right)]+8-\frac{2}{5}\)
Theo giả thiết \(\left(x+2\right)\left(y+2\right)=\frac{25}{4}\)
\(\Leftrightarrow xy+2\left(x+y\right)=\frac{9}{4}\)
\(\Rightarrow P\sqrt{17}\ge\frac{2}{5}.\frac{9}{4}+8-\frac{2}{5}=\frac{17}{2}\)
\(\Leftrightarrow P\ge\frac{\sqrt{17}}{2}\)
Điểm rơi \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Cho các số x,y thỏa mãn đẳng thức \(8x^2+y^2+\dfrac{1}{4x^2}=4\). Tìm GTLN, GTNN của biểu thức P = xy