Phương trình 2sin2x + sinx. cosx – cos2x = 0 có nghiệm là:
![]()

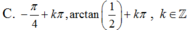
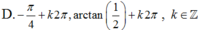
Phương trình 2 sin 2 x + sin x cos x - cos 2 x = 0 có nghiệm là:
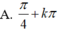


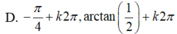
Phương trình 2sin2x - 3 6 |sinx + cosx| + 8 = 0 có nghiệm là
A. 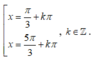
B. 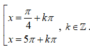
C. 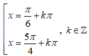
D. 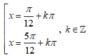
Cho phương trình: cos2x+(1+2cosx)(sinx-cosx)=0. Số họ nghiệm của phương trình dạng x = a + k 2 π là:
A.4
B.2
C.1
D.3
Cho phương trình: cosx+sinx=1+sin2x+cos2x. Nghiệm của phương trình có dạng x 1 = a π + k π x 2 = ± b π + k 2 π b > 0 . Tính tổng a + b
A. 1 12
B.3
C. 7 π 12
D. π 4
Số điểm biểu diễn nghiệm của phương trình cos 2 x + sinxcosx + cosx − sinx = 0 trên đường tròn lượng giác là
A. 4
B. 2
C. 1
D. 3
Đáp án C
Nhận thấy cos x = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được
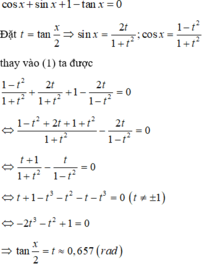
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Số điểm biểu diễn nghiệm của phương trình cos 2 x + sin x cos x + cos x - sin x = 0 trên đường tròn lượng giác là
A. 4
B. 2
C. 1
D. 3
Số điểm biểu diễn nghiệm của phương trình cos 2 x + sin x cos x + cos x - sin x = 0 trên đường tròn lượng giác là
A. 4
B. 2
C. 1
D. 3
Đáp án C
Nhận thấy cosx = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được
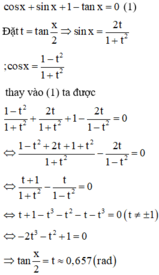
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi