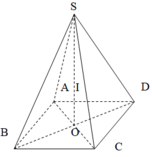
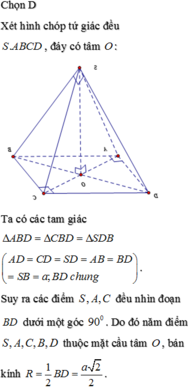
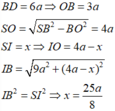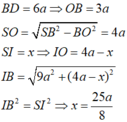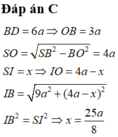Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.

Những câu hỏi liên quan
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. A.
2
a
14
7
B.
2
a
7
2
C.
2
a
7...
Đọc tiếp
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
A. 2 a 14 7
B. 2 a 7 2
C. 2 a 7 3 2
D. 2 a 2 7
Đáp án A
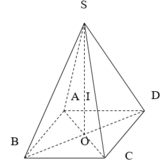
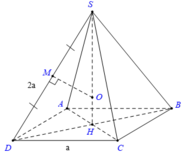
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông.
Gọi M là trung điểm của ABCD .
Trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O
Thì OS = OA = OC = OD
Nên O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
Bán kính mặt cầu là R = SO.
Ta có:
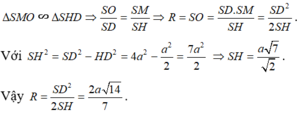
Đúng 0
Bình luận (0)
II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
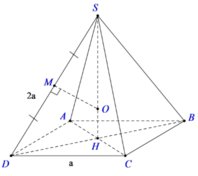
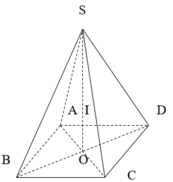
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC= OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có:

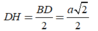
![]()
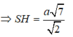
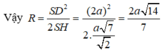
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy
3
2
a
,
bằng cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD. A.
R
3
a
.
B.
R...
Đọc tiếp
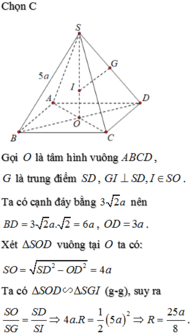
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy 3 2 a , bằng cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
A. R = 3 a .
B. R = 2 a .
C. R = 25 8 a .
D. R = 2 a .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
3
2
a
, cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2 a , cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
![]()
![]()
![]()
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
3
2
a
cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2 a cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
![]()
![]()
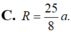
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
3
2
a
, cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD A.
R
3
a
B.
R
2
a
C.
R
25
8
a
D.
R
2
a
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2 a , cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
A. R = 3 a
B. R = 2 a
C. R = 25 8 a
D. R = 2 a
Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Bán kính mặt cầu ngoại tiếp hình chóp là:
Gọi G là trọng tâm đáy
tam giác ABC đều nên G cũng là tâm đường tròn ngoại tiếp đáy
suy ra AG=\(\frac{a}{\sqrt{3}}\).
Do SA=SB=SC=2a nên S cách đều A,B,C.từ đÓ SG vuông góc mp đáy tại G
Trong mp(SAG).gọi Mlà trung điểm SA,từ M kẻ đt vuông góc SA cắt SG tại I
nhận thấy I là tâm mặt cầu cần tìm
xét hai tam giác đồng dạng SMI vàSGA có
\(\frac{SM}{SG}=\frac{SI}{SA}\) từ đó suy ra R= SI=\(\frac{2a\sqrt{33}}{11}\)
Đúng 0
Bình luận (1)
Bán kính mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên cùng bằng a là
Đọc tiếp
Bán kính mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên cùng bằng a là
![]()
![]()
![]()
![]()
Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng
60
°
. A.
6
4
B.
6
2
C.
6
3
D.
6
6
Đọc tiếp
Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng 60 ° .
A. 6 4
B. 6 2
C. 6 3
D. 6 6
Đáp án C
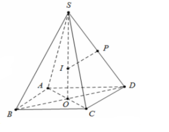
Kí hiệu như hình vẽ với IP là đường trung trực của đoạn thẳng S D ⇒ S I . S O = S P . S D ⇒ R = S D 2 2 S O .
Ta có tan 60 ° = S O O D = 3 ⇒ S O = 3 2 ⇒ S D = 2 ⇒ R = 6 3 .
Đúng 0
Bình luận (0)