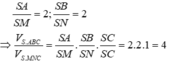Cho hình chóp S.ABC, gọi M; N lần lượt là trung điểm của SA; SB. Tính tỉ số V S . A B C V S . M N C
A. 1 2
B. 4
C. 2
D. 1 4
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các cạnh SA, BC. Trên cạnh AB lấy điểm K không trùng với trung điểm của AB. Tìm thiết diện của hình chóp S.ABC và (MNK)?
Thầy gợi ý cách xác định thiết diện thông qua hình vẽ sau:
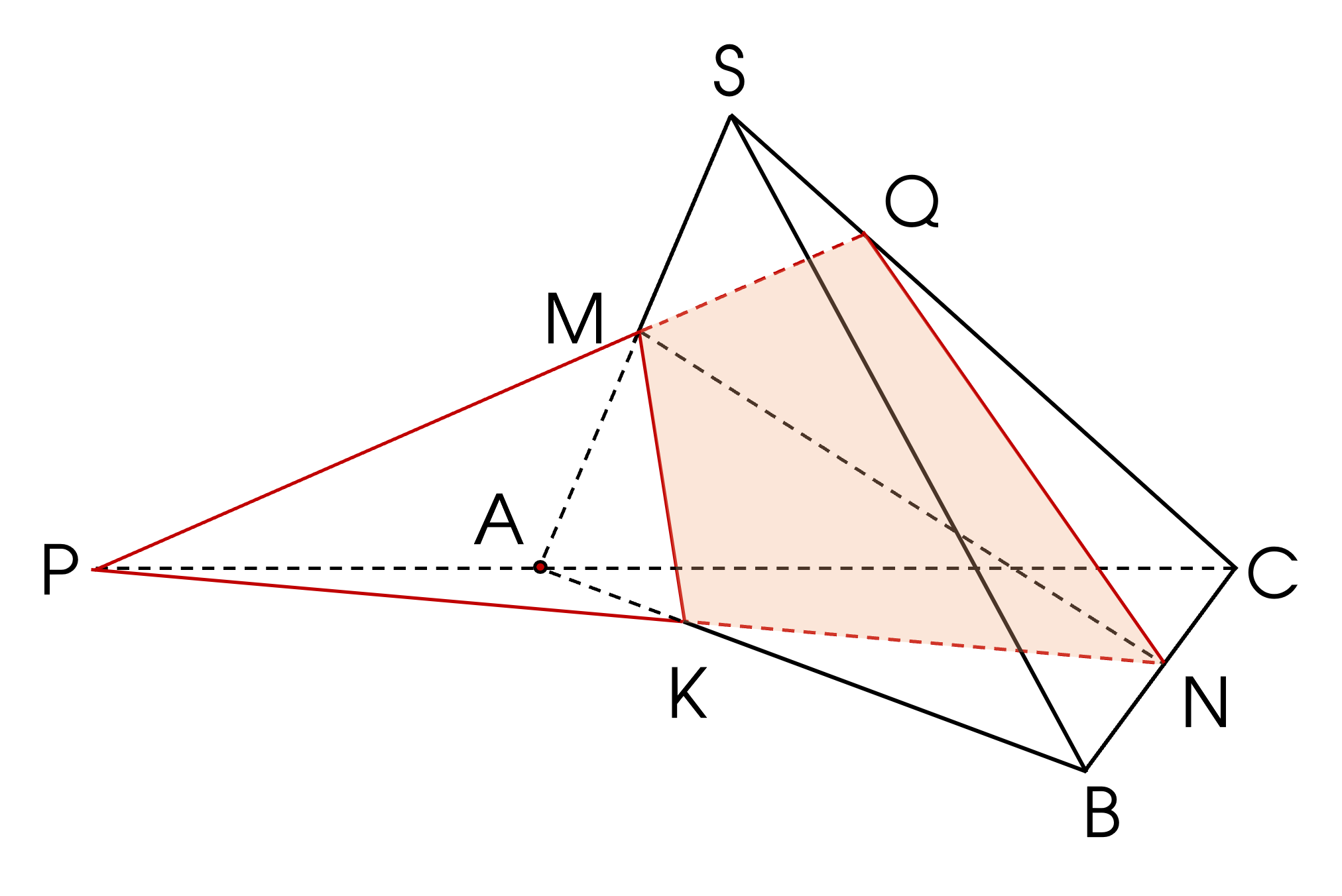
Em kéo dài KN cắt AC tại P (trong mp(ABC)), từ đó tiếp tục dựng hình để xác định giao tuyến với các mặt còn lại của hình chóp để có thiết diện là tứ giác KMQN nhé
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi M, N lần lượt là trung điểm của SB, SC. Biết A M N ⊥ S B C . Thể tích của khối chóp S.ABC bằng
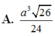
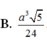
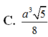
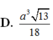
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi M, N lần lượt là trung điểm của SB, SC. Biết A M N ⊥ S B C . Thể tích của khối chóp S.ABC bằng
A. a 3 26 24
B. a 3 5 24
C. a 3 5 8
D. a 3 13 18
Cho hình chóp đều S.ABC có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của SA và SC. Biết rằng BM vuông góc với AN . Thể tích khối chóp S.ABC bằng:
A. 14 a 3 8
B. 3 a 3 4
C. 3 a 3 12
D. 14 a 3 24
Cho hình chóp tam giác đều S.ABC. Cho hình chóp tam giác đều S và có đường tròn đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là
A. 1 2
B. 1 4
C. 1 3
D. 2 3
Cho hình chóp tam giác đều S.ABC. Cho hình chóp tam giác đều S và có đường tròn đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là
A. 1 2
B. 1 4
C. 1 3
D. 2 3
Cho hình chóp S.ABC ,gọi M, N lần lượt là trung điểm của SA, SB . Tính tỉ số 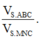
A. 4
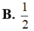
C.2
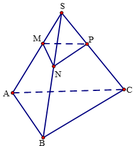
Cho hình chóp S . A B C có M là điểm di động trên cạnh SA sao cho S M S A = k . Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng A B C . Tìm k để mặt phẳng (α) cắt hình chóp S . A B C theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.
A. k = 2 2 .
B. k = 1 2 .
C. k = 3 2 .
D. k = 1 3 .
Đáp án A
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2
Cho hình chóp S.ABC, gọi M và N lần lượt là trung điểm của SA; SB. Tính tỉ số V S . A B C V S . M N C .
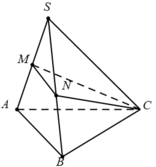
Do M và N lần lượt là trung điểm của SA và SB nên: