Hãy chứng minh định lý trên.
Những câu hỏi liên quan
Hãy chứng minh định lý trên.
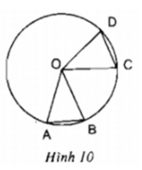
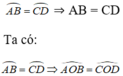
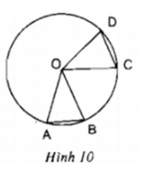
Xét ΔOAB và ΔOCD có:
OA = OC = R
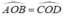
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
AB = CD ⇒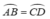 
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
Đúng 0
Bình luận (0)
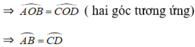
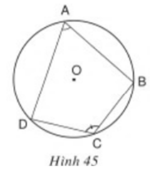
Xem hình 45. Hãy chứng minh định lý trên.
Theo tính chất góc nội tiếp chắn cung, ta có:
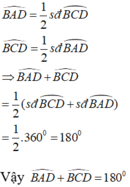
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o
Đúng 0
Bình luận (0)
Xem hình 45. Hãy chứng minh định lý trên.
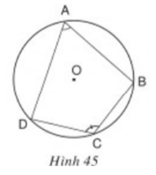
Theo tính chất góc nội tiếp chắn cung, ta có:
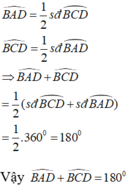
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180 °
Đúng 0
Bình luận (0)
Em hãy vẽ hình, viết giả thiết, kết luận và chứng minh định lý trên.
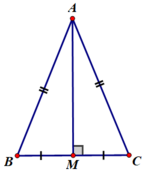
- Giả thiết : ΔABC cân tại A
AM là đường trung trực ứng với cạnh BC
- Kết luận : AM là trung tuyến ứng với cạnh BC
Đúng 0
Bình luận (0)
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
đ
B
n
C
⏜
+
s
đ
A
m...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh: B E C ^ = s đ B n C ⏜ + s đ A m D ⏜ 2
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
d
B
n
C
^
+
s
d
A
m
D
^...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B E C ^ = s d B n C ^ + s d A m D ^ 2
Hãy chứng minh Định lý 1.
Vì F(x) là nguyên hàm của f(x) trên K nên (F(x))' = f(x). Vì C là hằng số nên (C)’ = 0.
Ta có:
(G(x))' = (F(x) + C)' = (F(x))' + (C)' = f(x) + 0 = f(x)
Vậy G(x) là một nguyên hàm của f(x).
Đúng 0
Bình luận (0)
Xem hình 11.
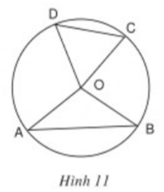
Hãy viết giả thiết và kết luận của định lý
(Không yêu cầu học sinh chứng minh định lý này)
Xem hình 11.
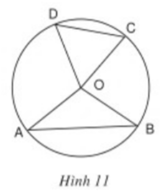
Hãy viết giả thiết và kết luận của định lý
(Không yêu cầu học sinh chứng minh định lý này)
