Các câu hỏi tương tự
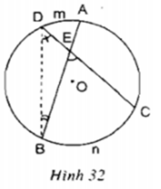
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
đ
B
n
C
⏜
+
s
đ
A
m...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh: B E C ^ = s đ B n C ⏜ + s đ A m D ⏜ 2
Cho hình vuông ABCD. Qua A kẽ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R, cắt CD tại Q và S.
a) chứng minh tam giác AQR và tam giác APS là hai tam giác cân.
b) QR cắt PS tại H; M, N là trung điểm của QR và PS. Chứng Minh tứ giác AMHN là hình chữ nhật.
c)Chứng minh P là trực tâm của AC.
d) Chứng minh bốn điểm M,B,N,D thẳng hàng
Cho tam giác ABC có ba góc nhọn (AB<AC). Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại M, N, BN cắt CM tại H.
a) Chứng minh AMHN nội tiếp, xác định tâm (I).
b) Đường tròn ngoại tiếp OCN cắt AO tại E. Chứng minh E thuộc đường tròn (I).
c) BC cắt AH tại D, cắt MN tại S. Chứng minh SM.SN=SD.SO
d) Chứng minh S, H, E thẳng hàng.
Hãy chứng minh định lí trên
Gợi ý: Sử dụng góc ngoài của tam giác trong ba trường hợp ở hình 36, 37, 38 ( các cung nêu ra dưới hình là những cung bị chắn).
Hãy chứng minh định lí trên
Gợi ý: Sử dụng góc ngoài của tam giác trong ba trường hợp ở hình 36, 37, 38 ( các cung nêu ra dưới hình là những cung bị chắn).
Cho đường tròn (O), điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyếnSM.SN (M, N là các tiếp điểm). Vẽ đường kính NA. a) Chứng minh OS vuông góc MN. b) So sánh MN với NΑ. c) Chứng minh AM//OS. d) Tính độ dài các cạnh của tam giác SMN, biết OM = 3(cm) 0S = 5(cm) HẾT.
Cho (O;R),điểm M ở ngoài (O) sao cho OM=2R.Vẽ tiếp tuyến MA,MB với (O),A>B là tiếp điểm.Lấy N tùy ý trên cung nhỏ AB.Gọi I,H,K lần lượt là hình chiếu vuông góc của N trên AB,AM,BM
a)tính SMAOB theo R
b)chứng minh góc NIH =góc NBA
c)gọi AN cắt IH tại E,BN cắt IK tại F
chứng minh IENF nội tiếp
d)giả sử O,N,M thẳng hàng
CM NA2+NB2=2R2
Cho tam giác ABC vuông tại A nội tiếp trong nửa đường tròn (O), đường cao AH. Gọi d và d lần lượt là hai tiếp tuyến của nửa đường tròn (O) tại B và C. Một điểm M thay đổi trên nửa đường tròn (O) (M khác B và C); đường thẳng qua M vuông góc với MH lần lượt cắt d và d tại E và F.a) Chứng minh HE vuông góc với HF.b) Gọi S là diện tích tam giác EHF. Chứng minh Sge AH^2Giups mk vs, tks nhìu.
Đọc tiếp
Cho tam giác ABC vuông tại A nội tiếp trong nửa đường tròn (O), đường cao AH. Gọi d và d' lần lượt là hai tiếp tuyến của nửa đường tròn (O) tại B và C. Một điểm M thay đổi trên nửa đường tròn (O) (M khác B và C); đường thẳng qua M vuông góc với MH lần lượt cắt d và d' tại E và F.
a) Chứng minh HE vuông góc với HF.
b) Gọi S là diện tích tam giác EHF. Chứng minh \(S\ge AH^2\)
Giups mk vs, tks nhìu.
Bài 3. Cho tam giác ABC vuông ở A, với AC AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Đọc tiếp
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE