Đường thẳng d có một vectơ chỉ phương là u → ( - 2 ; - 3 ) . Đường thẳng vuông góc với d có một vectơ pháp tuyến là:
A.(2;-3)
B. (4;6)
C. (6; 4)
D.(3; -2)
Đường thẳng d có một vectơ chỉ phương là u → = ( 3 ; - 4 ) . Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:
![]()
![]()
![]()
![]()
Đáp án A
Đường thẳng ( d) có VTCP là u → = ( 3 ; - 4 )
Nên đường thẳng (d) có 1 VTPT là ( 4; 3) .
Do 2 đườg thẳng ∆ và (d) song song với nhau nên chúng có cùng VTPT và cùng VTCP .
Suy ra đường thẳng ∆ có 1 VTPT là (4; 3) .
Đường thẳng d có một vectơ pháp tuyến là n→=(-4,-2). Trong các vectơ sau, vectơ nào là một vectơ chỉ phương của d ?
a. u→=(2,1)
b. u→=(2,4)
c. u→=(-2, 1)
d. u→=(-2, 4)
Đường thẳng d có một vectơ chỉ phương là u → ( 1 ; 3 ) . Trong các vectơ sau, vectơ nào là một vectơ pháp tuyến của d?
A.( 2; 6)
B. ( -1; -3)
C. ( 3; 1)
D. (6; -2)
Đường thẳng d có một vectơ pháp tuyến là n → = ( - 2 ; - 5 ) Đường thẳng ∆ song song với d có một vectơ chỉ phương là:
![]()
![]()
![]()
![]()
Đáp án A
Đường thẳng d có một vectơ pháp tuyến là n → = ( - 2 ; - 5 ) nên đường thẳng này có 1 VTCP là: n → = 5 ; - 2
Do đường thẳng d và ∆ song song với nhau nên vecto n → = ( 5 ; - 2 ) cũng là VTCP của đường thẳng ∆.
Đường thẳng (d) có một vectơ pháp tuyến là n → ( 2 ; - 1 ) . Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương là:
A. (2; -1)
B. (-1; 2)
C. (2; 1)
D.(1; 2)
Đáp án A
Do hai đường thẳng vuông góc với nhau thì VTPT của đường thẳng này là VTCP của đường thẳng kia và ngược lại.
Do đường thẳng ∆ vuông góc với đường thẳng (d) nên nhận VTPT của đường thẳng ( d) là VTCP. Do đó: một VTCP của đường thẳng ∆ là ( 2; -1)
hahahahahahahaha
câu trả lời là b
Đường thẳng d có một vectơ pháp tuyến là n → = - 2 ; - 5 . Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là:
A. u 1 → = ( 5 ; - 2 )
B. u 2 → = ( - 5 ; 2 )
C. u 3 → = ( 2 ; 5 )
D. u 4 → = ( 2 ; - 5 )
Chọn C.
Đường thẳng Δ vuông góc với d nhận VTPT của d là VTCP
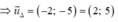
cho đường thẳng d có phương trình x=1-4t y=-3+t. Một vectơ chỉ phương của d là A. vectơ u=(1;-4) B.vectơ u=(4;1) C.vectơ u=(1;-3) D.vectơ u=(-4;1)
Ptr `d: {(x=1-4t),(y=-3+t):}`
`=>` Vtcp của `d` là: `\vec{u_d}=(-4;1)`
`->bb D`
Đường thẳng d có một vectơ pháp tuyến là 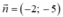 . Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là:
. Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là:
A. u → = ( 5 ; - 2 )
B. u → = ( - 5 ; 2 )
C. u → = ( 2 ; 5 )
D. u → = ( 2 ; - 5 )
Cho đường thẳng ∆ có vectơ chỉ phương là u → = 2 ; − 3 . Vectơ nào sau đây không phải là vectơ chỉ phương của ∆?
A. u 1 → = 3 ; 2
B. u 2 → = − 2 ; 3
C. u 3 → = 6 ; − 9
D. u 4 → = − 4 ; 6
ĐÁP ÁN A
Nếu u → là vectơ chỉ phương của một đường thẳng thì k u → (với k ≠ 0) đều là vectơ chỉ phương của đường thẳng đó.
Vì vậy các vectơ có tọa độ tỉ lệ với u → 2 ; - 3 đều là vectơ chỉ phương.
Ta có: 2 3 ≠ − 3 2 ; 2 − 2 = − 3 3 ; 2 6 = − 3 − 9 ; 2 − 4 = − 3 6
Do đó, trong các vecto đã cho có u 1 → không phải là vecto chỉ phương của đường thẳng ∆.