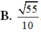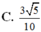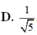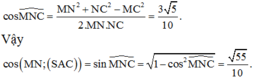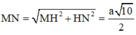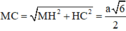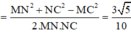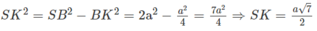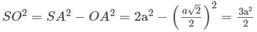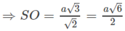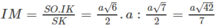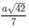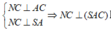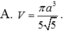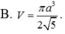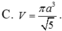Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
A. Ba đường thẳng A’B’, AB, CD đồng quy
B. Ba đường thẳng A’B’, AB, CD đồng quy hoặc đôi một song song
C. Trong ba đường thẳng A’B’, AB, CD có hai đường thẳng không thể cùng thuộc một mặt phẳng.
D. Ba đường thẳng A’B’, AB, CD đồng quy tại điểm thuộc mặt phẳng (SBC).