Đáp án B
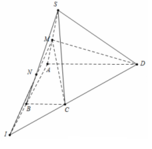
Gọi I = A B ∩ C D và N = S B ∩ M I khi đó giao điểm của SB và (MCD) là N. Dễ thấy MN và CD cắt nhau
Đáp án B

Gọi I = A B ∩ C D và N = S B ∩ M I khi đó giao điểm của SB và (MCD) là N. Dễ thấy MN và CD cắt nhau
Cho hình chóp SABCD có đáy ABCD là một tứ giác (AB không song song CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB, O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau
A. SO và AD
B. MN và SC
C. SA và BC
D. MN và SO
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, N lần lượt là hai trung điểm của AB, CD. Gọi (P) là mặt phẳng đi qua MN và cắt mặt bên (SBC) theo một giao tuyến. Thiết diện của (P) và hình chóp là:
A. Hình bình hành.
B. Hình chữ nhật.
C. hình thang.
D. Hình vuông.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA, N là điểm trên đoạn SB sao cho S N = 2 N B . Mặt phẳng chứa MN cắt đoạn SD tại Q và cắt đoạn SC tại P. Tỉ số V S . M N P Q V S . A B C D lớn nhất bằng
A. 2/5
B. 1/3
C. 1/4
D. 3/8
Cho hình chóp S.ABCD đáy ABCD là hình thang cân, A D = a , A B = a , B C = a , C D = 2 a . Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và SD. Tính cosin góc giữa MN và (SAC) biết thể tích khối chóp S.ABCD bằng a 3 3 4
A. 310 20
B. 3 5 10
C. 3 310 20
D. 5 10
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = a , A D = 2 a , S A vuông góc với mặt đáy A B C D , S A = a . Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC).
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại B. AB=BC=a, AD=2a. Biết SA vuông góc với đáy (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm SB,CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC)
A. 5 5
B. 55 10
C. 3 5 10
D. 2 5 5
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF.
A. V = a 3 6 36 .
B. V = a 3 6 9 .
C. V = a 3 6 6 .
D. V = a 3 6 18 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB = BC = CD = a, AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng a 3 3 4
A . 5 10
B . 3 310 20
C . 310 20
D . 3 5 10
Cho khối chóp S.ABCD có thể tích bằng 1, đáy ABCD là hình thang với cạnh đáy lớn là AD và AD = 3BC. Gọi M là trung điểm cạnh SA, N là điểm thuộc cạnh CD sao cho ND = 3NC. Mặt phẳng (BMN) cắt cạnh SD tại P. Tính thể tích khối chóp A.MBNP bằng
A. 3 8
B. 5 12
C. 5 16
D. 9 32