Cho tam giác ABC có AB < AC. Điểm D thuộc AC sao cho AD = AB. Gọi E là điểm nằm trong tam giác ABC sao cho EB = ED. Khi đó
A. Δ A B E = Δ A D E
B. Δ A E B = Δ A D E
C. Δ A B E = Δ D A E
D. A E D ^ = A B E ^
Cho tam giác ABC ( AB< AC ). Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh : a) Δ AIB = Δ CID. b) AD = BC và AD // BC. c) Gọi E là trung điểm của AB. Trên tia đối của tia EC lấy điểm K sao cho: EC = EK. Chứng minh: D, A, K thẳng hàng.
a) Xét Δ AIB và Δ CID:
+ IB = ID (gt).
+ IA = IC (I là trung điểm của AC).
+ ^AIB = ^CID (2 góc đối đỉnh).
=> Δ AIB = Δ CID (c - g - c).
b) Xét tứ giác ABCD có:
+ I là trung điểm của AC (gt).
+ I là trung điểm của BC (IB = ID).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AD = BC và AD // BC (Tính chất hình bình hành).
c) Xét tứ giác KABC có:
+ E là trung điểm của AB (gt).
+ E là trung điểm của KC (EC = EK).
=> Tứ giác KABC là hình bình hành (dhnb).
=> KA // BC (Tính chất hình bình hành).
Mà AD // BC (cmt).
=> 3 điểm D, A, K thẳng hàng (đpcm).
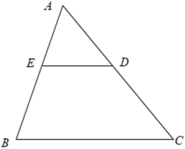
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Xét Δ AED và Δ ABC có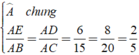
⇒ Δ AED ∼ Δ ABC ( c - g - c )
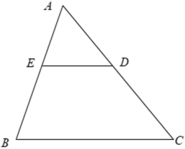
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Xét Δ AED và Δ ABC có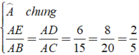
⇒ Δ AED ∼ Δ ABC ( c - g - c )
Cho tam giác ABC vuông ở A có AB=15cm, AC=20cm. Lấy điểm E nằm trên cạnh BC, sao cho EB=5cm. Từ điểm E kể ED và EF lần lượt vuông góc với AB và AC(D thuộc AB và F thuộc AC)
a) Tính độ dài các đoạn EC,DA,DB,FA,FC
b) Tính chu vi tam giác BDE, tam giác CEF
a: BC=căn 15^2+20^2=25cm
EC=25-5=20cm
ED//AC
=>BD/DA=BE/EC=1/4
=>BD/1=DA/4=15/5=3
=>BD=3cm; DA=12cm
EF//AB
=>FC/FA=EC/EB=4
=>FC/4=FA/1=20/5=4
=>FC=16cm; FA=4cm
b: DE=căn 5^2-3^2=4cm
=>C BDE=3+4+5=12cm
C CEF/C CAB=CE/CB=20/25=4/5
=>C CEF=4/5*(15+20+25)=4/5*60=48cm
cho tam giác ABC có AB<AC D là 1 điểm nằm giữa A C sao cho ABD=ACB a chứng minh 2 tam giác ABD và ACB đồng dạng b phân giác BAC cắt BD tại E cm ED/EB=AB/AC c cho biết AB=m AC=n tính theo m n tỉ số diện tích cảu 2 tam giác ABE và AE gì em ko nhớ
a,Xét \(\Delta\) ABD và \(\Delta\) ACB,ta có:
Góc ABD = góc ACB(gt)
Góc A-chung
=>\(\Delta\) ABD \(\sim\) \(\Delta\) ACB(g.g)(đpcm).
b,Xét \(\Delta\) ABD ,có đường phân giác AE:
=>\(\dfrac{ED}{AD}=\dfrac{EB}{AB}\) <=>\(\dfrac{ED}{EB}=\dfrac{AD}{AB}\) (1)
Ta có: \(\Delta\) ABD \(\sim\) \(\Delta\) ACB(câu a)
=>\(\dfrac{AD}{AB}=\dfrac{AB}{AC}\) (2)
Từ (1) và (2) =>\(\dfrac{ED}{EB}=\dfrac{AB}{AC}\) (đpcm).
c,-.-đùa à.
cho Δ ABC nhọn (AB <AC ) có ^A = 60 . D là TĐ của cạnh AC . Trên tia AB lấy điểm E / AE = AD . cm
a Δ ADE là Tam giác đều
b Δ DEC là tam giác cân
c CE ⊥ AB
Tam giác ABC vuông tại A, AB<AC. Trên cạnh AC lấy điểm D sao cho AB=AD. Trên tia đối tia AB lấy điểm E sao cho AE=AC.
a) Cm: Tam giác ABC = Tam giác ADE
b) Cm: ED⊥BC
c) Gọi H là giao điểm tia BD và ED. Cm: HB=HE
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
b: góc DEB+góc CBA=45+45=90 độ
=>DE vuông góc BC tại H
c: Sửa đề: H là giao của DE với BC
Xét ΔHEB vuông tại H có góc HEB=45 độ
nên ΔHEB vuông cân tại H
=>HE=HB
Tam giác ABC vuông tại A, AB<AC. Trên cạnh AC lấy điểm D sao cho AB=AD. Trên tia đối tia AB lấy điểm E sao cho AE=AC.
a) Cm: Tam giác ABC = Tam giác ADE
b) Cm: ED⊥BC
c) Gọi H là giao điểm tia BD và ED. Cm: HB=HE
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng: Δ ADC đối xứng với Δ AEB qua AH.
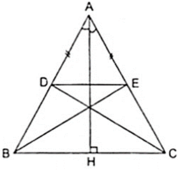
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.