Phương trình 2log3 (cotx) = log2 (cosx) có bao nhiêu nghiệm trong khoảng (0;2018π)?
A. 2018 nghiệm
B. 1008 nghiệm
C. 2017 nghiệm
D. 1009 nghiệm
Những câu hỏi liên quan
Hỏi phương trình 2log3 (cot x) log2 (cos x) có bao nhiêu nghiệm trong khoảng
0
;
2017
π
? A. 1009 nghiệm B. 1008 nghiệm C. 2017 nghiệm D. 2018 nghiệm
Đọc tiếp
Hỏi phương trình 2log3 (cot x) = log2 (cos x) có bao nhiêu nghiệm trong khoảng 0 ; 2017 π ?
A. 1009 nghiệm
B. 1008 nghiệm
C. 2017 nghiệm
D. 2018 nghiệm
Đáp án A
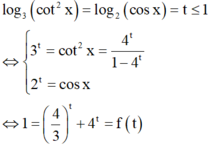
Dễ thấy f(t) là hàm số đồng biến trên TXD và f(–1) = 1 nên t = –1 là nghiệm duy nhất của phương trình f(t) = 1
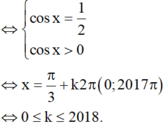
Vậy có 1009 nghiệm.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
log
2
cos
x
. Phương trình
f
x
0
có bao nhiêu nghiệm trong khoảng
0
;
2018
π
A. 1008 B. 1010 C. 2017 D. 2018
Đọc tiếp
Cho hàm số f x = log 2 cos x . Phương trình f ' x = 0 có bao nhiêu nghiệm trong khoảng 0 ; 2018 π
A. 1008
B. 1010
C. 2017
D. 2018
Nghiệm của phương trình log 4 { 2 log 3 [ 1 + log 2 ( 1 + 3 log 2 x ) ] } = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Phương trình
2
log
3
c
o
t
x
log
2
(
cos
x
)
có bao nhiêu nghiệm trong khoảng
0
;
2018
π
? A. 2018 nghiệm. B. 1008 nghiệm. C. 2017 nghiệm. D. 1009...
Đọc tiếp
Phương trình 2 log 3 c o t x = log 2 ( cos x ) có bao nhiêu nghiệm trong khoảng 0 ; 2018 π ?
A. 2018 nghiệm.
B. 1008 nghiệm.
C. 2017 nghiệm.
D. 1009 nghiệm.
Phương trình sin x + cos x = 1 có bao nhiêu nghiệm trên khoảng 0 ; π .
A. 1
B. 0
C. 2
D. 3
Phương trình cos 2 x + cos x = 0 có bao nhiêu nghiệm thuộc khoảng − π ; π
A. 1
B. 4
C. 2
D. 3
Đáp án C.
Phương pháp
Sử dụng tính chất hai góc bù nhau cos x = cos π − x
Giải phương trình lượng giác cơ bản
Cách giải
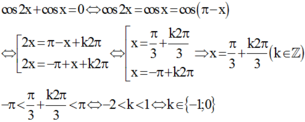
Vậy phương trình có 2 nghiệm thuộc − π ; π
Đúng 0
Bình luận (0)
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
Có bao nhiêu số nguyên trên [0; 10] nghiệm đúng bất phương trình log2(3x – 4) > log2 (x – 1)?
A. 9
B. 10
C. 8
D. 11
Có bao nhiêu số nguyên trên [0; 10] nghiệm đúng bất phương trình
log
2
(
3
x
-
4
)
log
2
(
x
-
1
)
A. 11 B. 8 C. 9 D. 10
Đọc tiếp
Có bao nhiêu số nguyên trên [0; 10] nghiệm đúng bất phương trình log 2 ( 3 x - 4 ) > log 2 ( x - 1 )
A. 11
B. 8
C. 9
D. 10
