Với giá trị nào của m thì hai đường thẳng d1: 4x -3y + 3m= 0 và d 2 : x = 1 + 2 t y = 4 + m t trùng nhau ?
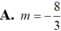

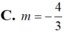
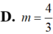
Với giá trị nào của m thì hai đường thẳng d 1 : x = 2 + 2 t y = 1 + m t và d2 : 4x – 3y + m= 0 trùng nhau ?
A.m= 1
B.m= -1
C.m= 2
D.không có m thỏa mãn
Đáp án D
Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi:
Hệ phương trình
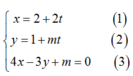 có vô số nghiệm.
có vô số nghiệm.
Thay (1) ; (2) vào (3) ta được : 4 (2+ 2t) -3 (1+ mt) + m= 0
Hay ( 3m- 8)t = m+5 (*)
Phương trình (*) có vô số nghiệm khi và chỉ khi
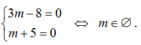
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
![]()
![]()
![]()
![]()
Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 = 0 và d 2 : x = 1 + 2 t y = 7 - m t vuông góc với nhau?
A. m = 3 2
B. m = 3
C. m = -3
D. m = - 3 2
Bài 8. Cho các đường thẳng (d1) : y 4mx - (m+5) với m≠0 =
(d_{2}) / y = (3m ^ 2 + 1) * x + (m ^ 2 - 9)
a) Với giá trị nào của m thì (di) song song với đường thẳng (d2)
b) Với giá trị nào của m thì (d1) cắt (d2) tìm toạ độ giao điểm khi m = 2
c) C/m rằng khi m thay đổi thì đường thẳng (d1) luôn đi điểm cố định A.
a: Để hai đường song song thì \(\left\{{}\begin{matrix}3m^2+1=4m\\-m-5< >m^2-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3m^2-4m+1=0\\m^2-9+m+5< >0\end{matrix}\right.\)
\(\Leftrightarrow m\in\left\{1;\dfrac{1}{3}\right\}\)
b: Khi m=2 thì (d1): y=8x-7
(d2): \(y=\left(3\cdot2^2+1\right)\cdot x+\left(2^2-9\right)=13x-5\)
Tọa độ giao điểm là:
13x-5=8x-7 và y=8x-7
=>x=-2/5 và y=-16/5-7=-51/5
1.a) Với giá trị nào của m thì hai đường thẳng y= 2x + 3 + m và y= 3x + 5 - m, cắt nhau tại một điểm trên trục tung
b) Viết phương trình đường thẳng (d) biết (d) song song với (d'): y = \(\dfrac{-1}{2}x\) và cắt trục hoành tại điểm có hoành độ bằng 10
2. Cho các đường thẳng (d1): y= 4mx - (m + 5) với (m\(\ne\)0)
(d2): y= (3m + 1) x + (m - 9)
a) Với giá trị nào của m thì ( d1) // (d2)
b) Với giá trị nào của m thì (d1) cắt (d2). Tìm tọa độ giao điểm khi m = 2
Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)
Trong mặt phẳng Oxy, cho hai đường thẳng y=mx+3m+2 và (d1) y=x+1. Tìm giá trị của m để đường thẳng (d) và (d1) song song với nhau
Để hai đường thẳng song song mà không trùng nhau thì điều kiện cần và đủ là :
\(\hept{\begin{cases}m=1\\3m+2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\m\ne-\frac{1}{3}\end{cases}\Leftrightarrow}m=1}\)
cho đường thẳng d: y = (2m+3)x - 3m +4. tìm các giá trị của tham số m để d đi qua giao điểm của 2 đường thẳng d1: 2x - 3y =12 và d2: 3x + 4y =1
Tọa độ giao điểm của hai đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-3y=12\\3x+4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-12y=48\\9x+12y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17x=51\\3x+4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\4y=1-3x=1-3\cdot3=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Thay x=3 và y=-2 vào (d), ta được:
\(3\left(2m+3\right)-3m+4=-2\)
=>6m+9-3m+4=-2
=>6m+13=-2
=>6m=-15
=>\(m=-\dfrac{5}{2}\)
với giá trị nào của m thì hai đường thẳng d1:2x+y+4-m=0 và d2:(m+3)x+y+2m-1=0
Thì hai đường thẳng thế nào hả bạn?
Với giá trị nào của m thì ba đường thẳng phân biệt d 1 : y = ( m + 2 ) x – 3 m − 3 ; d 2 : y = x + 2 v à d 3 : y = m x + 2 giao nhau tại một điểm?
A. m = 1 3
B. m = - 5 3
C. m = 1 ; m = − 5 3 ;
D. m = − 5 6
Để 3 đường thẳng trên là ba đường thẳng phân biệt thì m + 2 ≠ 1 m ≠ 1 m ≠ m + 2 ⇔ m ≠ 1 m ≠ − 1
Xét phương trình hoành độ giao điểm của d 2 v à d 3 :
x + 2 = m x + 2 ⇔ x ( m – 1 ) = 0 x = 0 m = 1 ( k t m )
Với x = 0 y = 2 nên giao điểm của d 2 ; d 3 là M (0; 2)
Để ba đường thẳng trên giao nhau tại 1 điểm thì M ∈ d 1 nên:
2 = ( m + 2 ) . 0 – 3 m – 3 ⇔ 3 m = − 5 ⇔ m = − 5 3 ( t m )
Vậy m = − 5 3
Đáp án cần chọn là: B