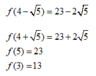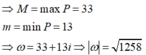Tính mô-đun của số phức z, biết ![]() và z có phần thực dương.
và z có phần thực dương.
A. 2
B. 1
C.3
D. 5
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Tính mô-đun của số phức ω = 1 - z + z 2 bằng
A. ![]() .
.
B.![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Gọi z=a+bi a ∈ ℝ , b ∈ ℝ , ta có:
![]()
![]()
![]()
![]()
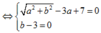
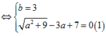
Giải (1) ta có:
![]()
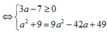
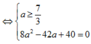
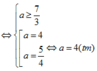
Do đó a=4; b=3; ⇒ z=4+3i
Khi đó
![]()
=1-4-3i+16+24i-9=4-21i
Vậy w = 4 2 + - 21 2 = 457 .
Chọn đáp án D.
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z - z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z + z 2 bằng
![]()
![]()
![]()
![]()
Cho số phức z có phần ảo gấp hai phần thực và z + 1 = 2 5 5 . Khi đó mô đun của z là
A. 4
B. 6
C. 2 5
D. 5 5
Chọn D
Số phức z có dạng z = a + 2ai (a ∈ R)
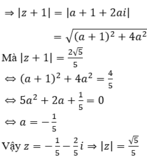
Cho hai số phức z = 5 + 2 i v à z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 5.
B. 3 5
C. 17
D. 37
Chọn đáp án A
Ta có w = z - z ' = 4 + 3 i
⇒ w = 4 2 + 3 2 = 5
Cho hai số phức z = 5 + 2 i và z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 7(cm)
B. 3(cm)
C. 6(cm)
D. 2(cm)
Chọn đáp án B
Gọi các kích thước của khối hộp là a (cm), b(cm), c (cm) với a, b, c là các số nguyên dương.
Từ giả thiết ta có
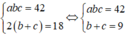
Lại có 9 = b + c ≥ 2 b c ⇒ b c ≤ 81 4
Mà b, c là các số nguyên dương nên b c ≤ 20
Từ b +c =9
⇒ trong hai số b, c có 1 số lẻ và 1 số chẵn ⇒ bc chẵn.
Từ a = 42 b c và a nguyên dương nên bc là ước nguyên dương của 42.

Nếu bc =6 thì b, c là nghiệm của phương trình X 2 - 9 X + 6 = 0 (loại vì nghiệm của phương trình này không là số nguyên).
Nếu bc =14 thì b, c là nghiệm của phương trình
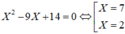
⇒ b c = 14 thỏa mãn. Vậy chiều cao của khối hộp là a = 42 b c = 3 c m
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính mô đun của số phức z + i.
A. z + i = 61
B. z + i = 5 2
C. z + i = 3 5
D. z + i = 2 41
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - 1 | 2 . Tính mô đun của số phức ω = M + mi
A. | ω | = 1258
B. | ω | = 3 137
C. | ω | = 2 134
D. | ω | = 2 309
Đáp án A
Đặt z = x + yi
Có ![]()
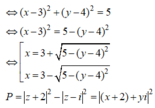
![]()
TH1:
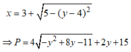
Xét hàm số: ![]() trên
trên ![]()
Có

Ta có:
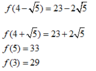
TH2:
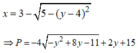
Xét hàm số: ![]() trên
trên ![]()
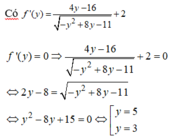
Ta có: