Đặt log126=a và log127=b Hãy biểu diễn log27 theo a và b
A. log 2 7 = a 1 - b
B. log 2 7 = a 1 + b
C. log 2 7 = b 1 - a
D. log 2 7 = a a - 1
Đặt log 12 6 = a và log 12 7 = b . Hãy biểu diễn log 2 7 theo a và b
![]()
![]()
![]()
![]()
Đặt a = log 12 6 , b = log 2 7 . Hãy biểu diễn log 12 7 theo a và b.
A. b a + 1 .
B. b 1 − a .
C. a b − 1 .
D. a b + 1 .
Đáp án B
Phương pháp giải:
Biểu diễn số theo hai giá trị của giả thiết qua các công thức thường sử dụng
Lời giải:
Ta có log 12 6 = log 12 12 2 = 1 − log 12 2 = a ⇒ log 12 2 = 1 − a
Vậy log 12 7 = log 12 7 log 12 2 = b 1 − a
Đặt a = log 12 6 , b = log 2 7 . Hãy biểu diễn log 2 7 theo a và b.
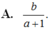
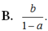
![]()
![]()
Nếu log 12 6 = a và log 12 7 = b thì log 2 7 bằng kết quả nào sau đây?
A. a a − 1
B. b 1 − a
C. a 1 + b
D. a 1 − b
Đáp án B
Ta có: log 2 7 = log 12 7 log 12 2 = log 12 7 log 12 12 6 = log 12 7 1 − log 12 6 = b 1 − a
Cho log 12 6 = a ; log 12 7 . Hãy tính log 2 7
A. a a - 1
B. a 1 - b
C. a 1 + b
D. b 1 - a
Ta có a = log 12 6 < 1 ; b = log 12 7 < 1 . Suy ra a 1 - a < 0. Do đó (A) sai.
Rõ ràng b > a > 0 ⇒ a 1 + b < 1 Do đó (C) sai.
Mặt khác log 2 7 = log 12 7 log 12 2 = b 1 - a
Vậy (D) là phương án đúng
Đáp án D
Đặt a = log 7 11 , b = log 2 7 . Hãy biểu diễn log 7 3 121 8 theo a và b.
A. log 7 3 121 8 = 6 a + 9 b
B. log 7 3 121 8 = 6 a - 9 b
C. log 7 3 121 8 = 6 a - 9 b
D. log 7 3 121 8 = 2 3 a - 9 b
Đặt a = log 2 5 , b = log 3 5 . Hãy biểu diễn log 6 5 theo a và b.
A. log 6 5 = 1 a + b
B. log 6 5 = a b a + b
C. log 6 5 = a 2 + b 2
D. log 6 5 = a + b
Nếu log 12 6 = a và log 12 7 = b thì
A. log 2 7 = b 1 + a
B. log 2 7 = 1 − a b
C. log 2 7 = 1 − a b
D. log 2 7 = 1 + a b
Nếu log 12 6 = a và log 12 7 = b thì
A. log 2 7 = b 1 + a
B. log 2 7 = b 1 - a
C. log 2 7 = 1 + a b
D. log 2 7 = 1 - a b