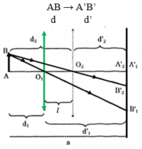
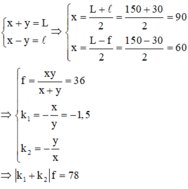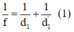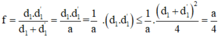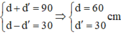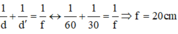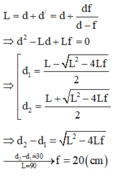Vật sáng AB cách màn ảnh 150cm. Trong khoảng giữa vật và màn ta đặt một thấu kính hội tụ O coi như song song với vật AB. Di chuyển O dọc theo trục chính, ta thấy có hai vị trí của O cho ảnh hiện rõ trên màn. Hai vị trí cách nhau 30cm. Tiêu cự của thấu kính là
A. 36cm
B. 12cm
C. 24cm
D. 20cm