Trong không gian Oxyz, cho mặt phẳng (P): 2x + y + 2z + 2 =0 và cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) là
A. 7
B. 10
C. 3
D. 1
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
A. 4π
B. π
C. 2π
D. 16π
Đáp án A
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n → (2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
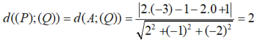
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu: 2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4π R 2 = 4 π
Trong không gian Oxyz, cho hai mặt phẳng P : 2 x - y + 2 z - 4 = 0 và Q : 2 x - y + 2 z + 5 = 0 . Mặt cầu (S) tiếp xúc với hai mặt phẳng (P) và (Q) có bán kính bằng
A. 3
B. 3 2
C. 9
D. 1 2
Trong không gian Oxyz, cho hai mặt phẳng P : 2 x - y + 2 z - 4 = 0 và Q : 2 x - y + 2 z + 5 = 0 . Mặt cầu S tiếp xúc với hai mặt phẳng P và Q có bán kính bằng
A. 3
B. 3 2
C. 9
D. 1 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Trong không gian Oxyz, cho mặt cầu S : x - a 2 + y - 2 2 + z - 3 2 = 9 và mặt phẳng ( P ) : 2 x + y + 2 z – 1 = 0 . Giá trị của a để (P) cắt mặt cầu (S) theo đường tròn (C)
A. - 17 2 ≤ a ≤ 1 2
B. - 17 2 < a < 1 2
C. -8 < a < 1
D. - 8 ≤ a ≤ 1
Chọn C.
S : x - a 2 + y - 2 2 + z - 3 2 = 9 có tâm I(a;2;3) và có bán kính R = 3
Để (P) cắt mặt cầu (S) theo đường tròn (C)
![]()
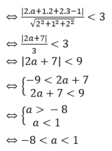
Trong không gian với hệ trục Oxyz, cho mặt phẳng P : 2 x + y + 2 z + 2 = 0 và cho mặt cầu S : x - 2 2 + y - 1 2 + z - 1 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) bằng.
A. 7
B. 10
C. 3
D. 1
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:
A. r = 6
B. r = 2 2
C. r = 4
D. r = 2 3
Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là 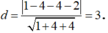
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: ![]()
Trong không gian Oxyz, cho điểm I(4;0;1) và mặt phẳng P : 2 x - y + 2 z - 1 = 0 . Phương trình mặt cầu (S ) có tâm I và tiếp xúc với mặt phẳng (P) là
A. x - 4 2 + y 2 + z - 1 2 = 3
B. x + 4 2 + y 2 + z + 1 2 = 3
C. x - 4 2 + y 2 + z - 1 2 = 9
D. x + 4 2 + y 2 + z + 1 2 = 9
Trong không gian Oxyz, cho điểm I(4;0;1) và mặt phẳng P : 2 x - y + 2 z - 1 = 0 . Phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P) là
![]()
![]()
![]()
![]()