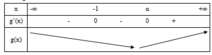
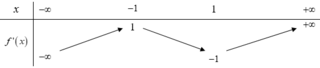
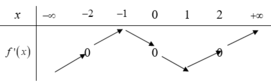
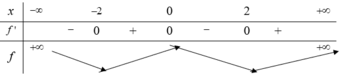
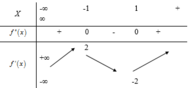
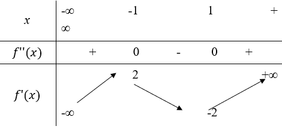
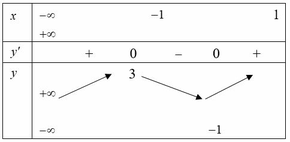
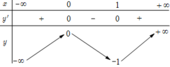
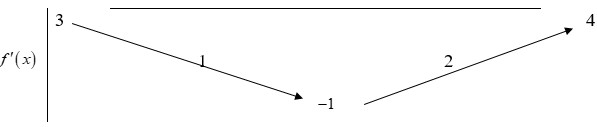
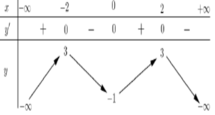
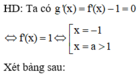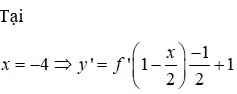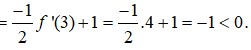Cho hàm số y = f(x) có bảng biến thiên như hình vẽ
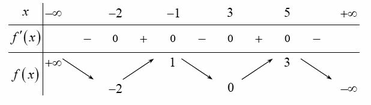 Xét hàm số
g
x
=
f
x
-
4
+
2018
2019
. Số điểm cực trị của hàm số y = g(x) bằng
Xét hàm số
g
x
=
f
x
-
4
+
2018
2019
. Số điểm cực trị của hàm số y = g(x) bằng
A. 9.
B. 1.
C. 5.
D. 2.