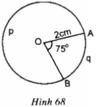
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính sđ A p B ⏜
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc A O B = 75 °
a) Tính sđ góc ApB
b) Tính độ dài hai cung AqB và ApB
c) Tính diện tích hình quạt tròn OAqB
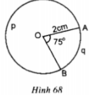
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính diện tích hình quạt tròn OAqB
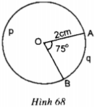
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính độ dài hai cung AqB và ApB

Vẽ đường tròn (O;2cm). Gọi A là một điểm nằm ngoài đường tròn (O;2cm). OA cắt đường tròn (O;2cm) ở B biết OA= 3 cm.
a) Tính AB
b) vẽ đường tròn tâm B bán kính BA. Hỏi điểm O có nằm trong đường tròn tâm B bán kính AB không? Vì sao?
c) đường tròn tâm B bán kính BA cắt đường tròn tâm O bán kính 2cm ở P và Q, cắt OA ở K. Chứng tỏ K nằm trong đường tròn tâm O bán kính 2 cm
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
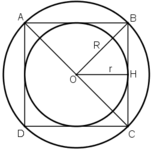
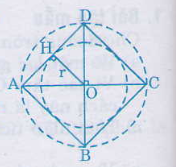
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 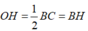
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
bài 1: cho đường tròn tâm /o bán kính 2cm. Góc SOB =60.
a) tính sđ cung AmB
b) tính độ dài hai cung AnB và AmB, độ dài đường tròn tâm O
c) tính diện tích hình tròn, diện tích hình quạt tròn OAnB.
bài 2: cho tam giác ABC có 3 góc nhọn. Đừng tròn tâm O đường kính BC cắt AB, AC lần lượt tại I và K. BK và CI cắt nhua tại H. Tia AH cắt BC tại M.
a) chứng minh \(AM\perp BC\)
b) chứng minh tứ giác BIHM, CMHK, AKMB nội tiếp. xác định tâm đường tròn ngoại tiếp
Vẽ đường tròn tâm O và tâm I bán kính 2cm, trong đó điểm I nằm trên đường tròn (O) và cắt nhau tại A, B.
a) Vẽ các đường tròn tâm A, tâm B bán kính 2cm.
b) Hai đường tròn trên có đi qua O và I không? Chúng có cắt nhau không? Vì sao?
a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.
Vẽ đường tròn tâm O và tâm I bán kính 2cm, trong đó điểm I nằm trên đường tròn (O) và cắt nhau tại A, B.
a) Vẽ các đường tròn tâm A, tâm B bán kính 2cm.
b) Hai đường tròn trên có đi qua O và I không? Chúng có cắt nhau không? Vì sao?
a) HS tự vẽ hình.
b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.